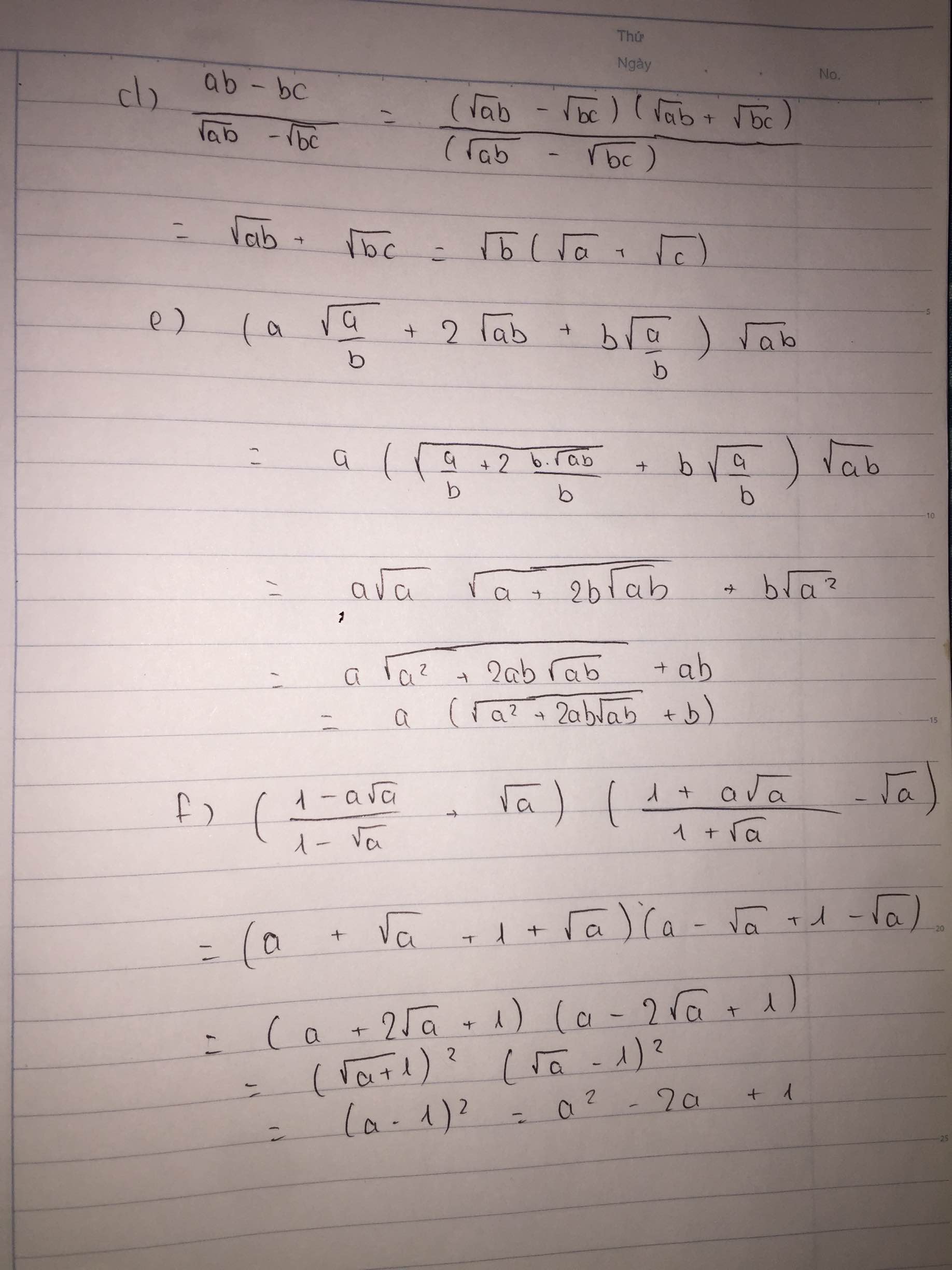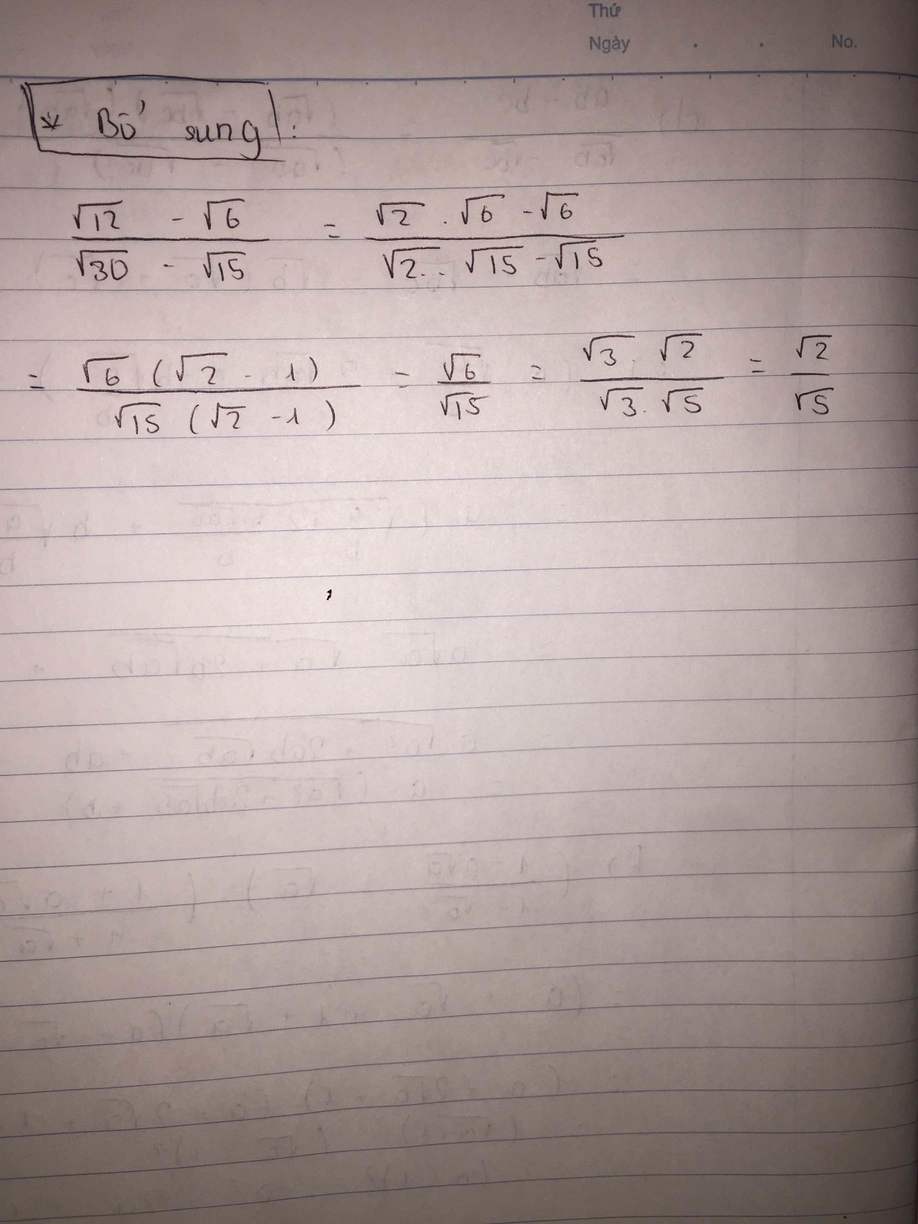Giusp em với mng oiq! em cảm ơn rất nhiều ạ!!
HA
Những câu hỏi liên quan
Giusp em bài này với mọi người ạ, em cảm ơn rất nhiều ạ.

a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giusp em thực hiện bài này được không ạ, em cảm ơn rất nhiều ạ!!!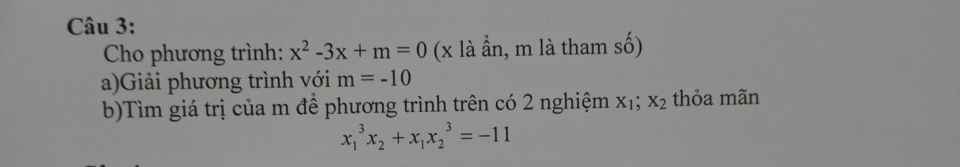
a)\(x^2+3x-10=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Mong mng giúp em vơi ạ. Em cảm ơn mng rất nhiều ❤️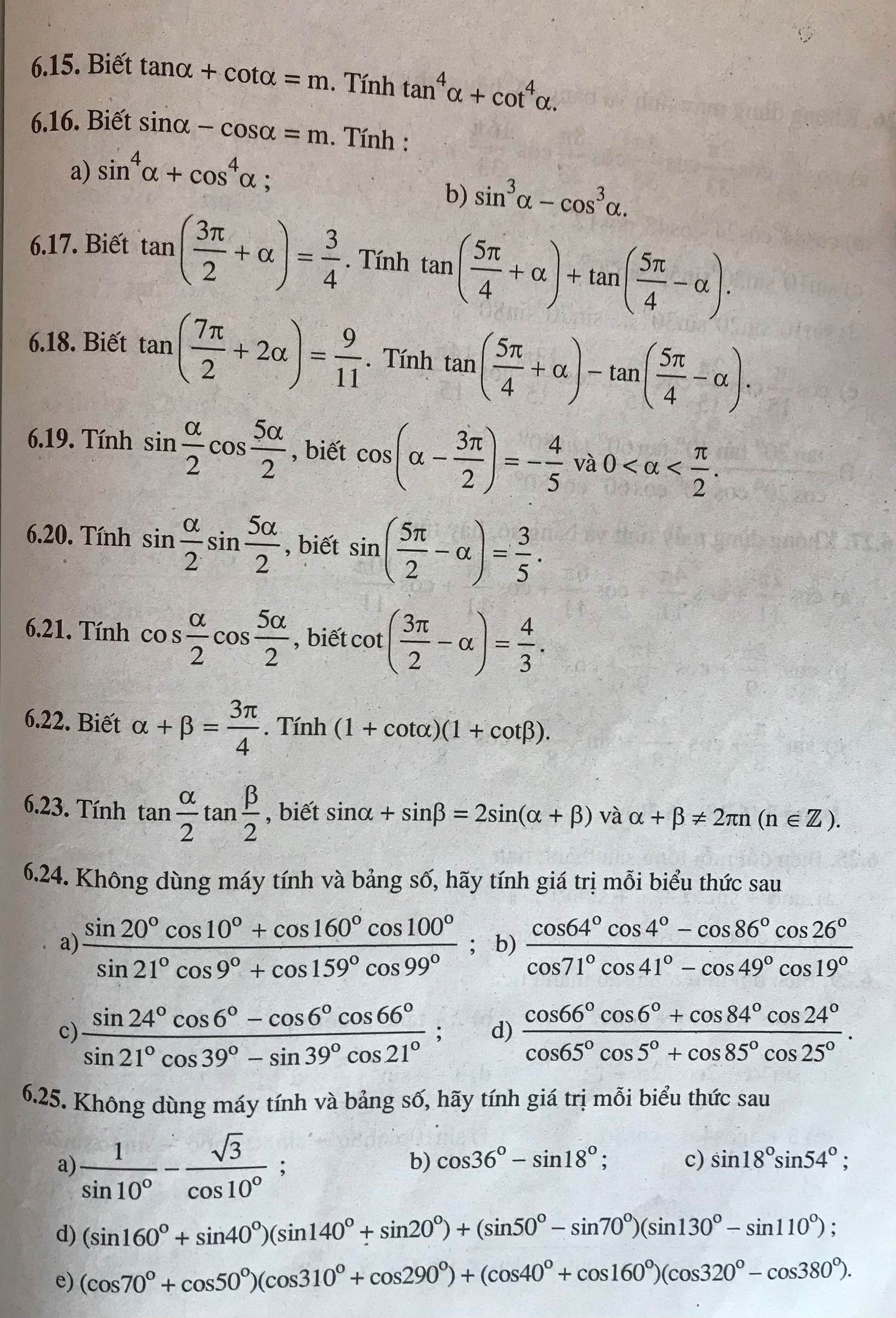
Mọi người ơi, giúp em bài này vớ ạ, em đang cần gấp lắm ạ, cảm ơn mng rất rất nhiều ạ.
Giusp mình với mọi người ơi!!!
Đúng 0
Bình luận (0)
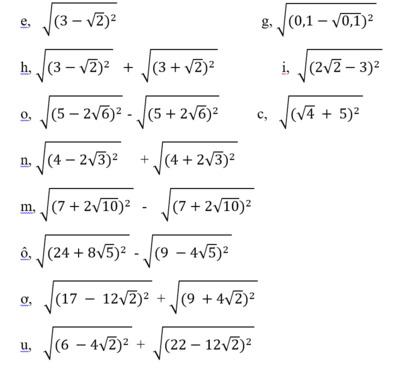
Thực hiện phép tính. Giusp mình nhanh với mng ạ@!!!! Mình cảm ơn nhiều.
e: \(=\left|3-\sqrt{2}\right|=3-\sqrt{2}\)
h: \(=3-\sqrt{2}+3+\sqrt{2}=6\)
g: \(=\left|0.1-\sqrt{0.1}\right|=0.1-\sqrt{0.1}\)
i: \(=\left|2\sqrt{2}-3\right|=3-2\sqrt{2}\)
c: \(=\left|2+5\right|=7\)
o: \(=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\)
n: \(=4-2\sqrt{3}+4+2\sqrt{3}=8\)
m: \(=7+2\sqrt{10}-7-2\sqrt{10}=0\)
Đúng 0
Bình luận (0)

GIÚP EM VS Ạ CẢM ƠN MNG RẤT NHIỀU KO CẦN LM CÂU 1 VS CÂU 2 ĐÂU Ạ :(( CẢM ƠN :3
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5
Đúng 0
Bình luận (0)
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Đúng 1
Bình luận (0)
Mng giúp em với, em cảm ơn nhiều ạ
Câu 28: C
Câu 27: D
Câu 26: C
Câu 25: B
Đúng 1
Bình luận (0)