giá trị lớn nhất của biểu thức:
A=\(\frac{10}{\left(x+2\right)^2+5}\)là
Giá trị lớn nhất của biểu thức :
A=\(\frac{10}{\left(x+2\right)^2+5}\)là
A lớn nhất <=>(x+2)2+5 nhỏ nhất
Ta có:(x+2)2\(\ge\)0 với mọi x
=>(x+2)2+5\(\ge\)5
Hay Min (x+2)2+5=5 khi x=-2
Vậy Max A=10/5=2 khi x=-2
cho biểu thức \(A=33×3+720:\left(x-6\right)\)
Tìm giá trị của x khi \(A=139\)
Tìm giá trị số tự nhiên của x để biểu thức A có giá trị lớn nhất, giá trị lớn nhất là bao nhiêu?
\(A=139\)
\(\Leftrightarrow720:\left(x-6\right)=40\)
\(\Leftrightarrow x-6=18\)
hay x=24
Giá trị lớn nhất của biểu thức \(A=\frac{\left|x\right|+5}{2\left|x\right|+3}\) là bao nhiêu?
( Nhập kết quả dưới dạng phân số tối giản )
A chắc chắn phải dương, vì cả tử và mẫu đều cùng dấu dương.
Do đó khi 2A lớn nhất thì A cũng lớn nhất.
\(2A=\frac{2\left|x\right|+10}{2\left|x\right|+3}=1+\frac{7}{2\left|x\right|+3}\)
Để 2A lớn nhất thì \(\frac{7}{2\left|x\right|+3}\) lớn nhất. 7 là số nguyên dương nên để phân số này lớn nhất thì 2|x|+3 là số dương bé nhất có thể.
|x| > 0
\(\Rightarrow\)2|x| > 0
\(\Rightarrow\)2|x|+ 3 > 3
\(\Rightarrow2A\) lớn nhất là \(1+\frac{7}{3}=\frac{10}{3}\)
Do đó A lớn nhất là \(\frac{10}{3}:2=\frac{5}{3}\)
Giá trị lớn nhất của biểu thức:\(\frac{x^2+15}{x^2+3}\)là:...
Ta có:
x2 + 15/x2 + 3 = x2 + 3/x2 + 3 + 12/x2 + 3 = 1 + 12/x2 + 3
Để biểu thức trên đạt GTLN thì 12/x2 + 3 đạt GTLN
=> x2 + 3 đạt GTNN
Mà x2 + 3 > hoặc = 3
Dấu "=" xảy ra khi và chỉ khi x = 0
=> GTLN của biểu thức: x2 + 15/x2 + 3 = 0 + 15/0 + 3 = 15/3 = 5
Đặt: \(M=\frac{x^2+15}{x^2+3}=\frac{x^2+3+12}{x^2+3}=\frac{x^2+3}{x^2+3}+\frac{12}{x^2+3}=1+\frac{12}{x^2+3}\)
Để M đạt GTLN thì \(x^2+3\) đạt giá trị nhỏ nhất.
Có: \(x^2\ge0\Rightarrow x^2+3\ge3\)
Dấu bằng xảy ra hi: \(x^2+3=3\Rightarrow x^2=0\Rightarrow x=0\)
Thay vào: \(M=1+\frac{12}{0^2+3}=1+\frac{12}{3}=1+4=5\)
Vậy: \(Max_M=5\) tại \(x=0\)
1. Tìm giá trị nhỏ nhất của biểu thức P=(x+3)2 + (y-1/3)4 - 4
2. Tìm giá trị lớn nhất của biểu thức Q= \(\frac{7}{\left(3x-2\right)+2016}\)
Tìm giá trị lớn nhất của biểu thức \(B=9-\left|x-\frac{1}{2}\right|\)
\(B=9-\left|x-\frac{1}{2}\right|\)
Vì : \(-\left|x-\frac{1}{2}\right|\le9\)
=> \(9-\left|x-\frac{1}{2}\right|\le9\)
Vậy GTLN của B là 9 khi \(x=\frac{1}{2}\)
Ta có : \(\left|x-\frac{1}{2}\right|\ge0\Rightarrow-\left|x-\frac{1}{2}\right|\le0\Rightarrow9-\left|x-\frac{1}{2}\right|\le9\)
Dấu "=" xảy ra \(\Leftrightarrow\left|x-\frac{1}{2}\right|=0\Leftrightarrow x=\frac{1}{2}\)
Vậy Max B = 9 <=> x = 1/2
Ta có
\(\left|x-\frac{1}{2}\right|\ge0\) với mọi x
\(-\left|x-\frac{1}{2}\right|\le0\)
\(9-\left|x-\frac{1}{2}\right|\le9\)
Dấu " = " xảy ra khi \(x=\frac{1}{2}\)
Vậy MAX A = 9 khi x=1/2
Giá trị lớn nhất của biểu thức A = - ( -x2 - 5)2 là ?
làm
5. Tìm giá trị nhỏ nhất của B= (x+1)2 + (y+3)2+1
Ai nhanh mk tick cho
ghi rõ cách làm nha
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
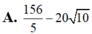
![]()
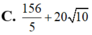
![]()