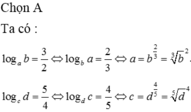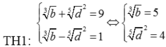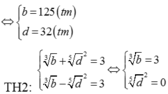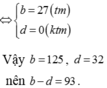Cho các số dương a, b, c, d và a/1+a + b/1+b + c/1+c + d/1+d <= 1. Chứng minh rằng a*b*c*d <= 1/81
H24
Những câu hỏi liên quan
Cho 4 số nguyên a, b, c, d (b, d < 0) và (a, b) = (c, d) = 1
a) Chứng minh nếu a/b + c/d thuộc Z thì b=d
b) Tìm các số dương a, b, c thỏa 1/a + 1/b + 1/c thuộc Z
1.cho a,b,c là các số dương lớn hơn 1.Chứng minh a^2/(b-1)+b^2/(c-1)+c^2/(a-1)>=12
2.Cho các số tự nhiên a,b,c,d. Chứng minh rằng M=a/(a+b+c)+b/(b+c+d)+c/(c+d+a)+d/(d+a+b) không là số tự nhiên
Câu hỏi của Adminbird - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
1)Cho 1/c=1/2(1/a + 1/b) với a,b,c khác 0 và b khác c.CMR: a/b=a-c/c-b
2)Cho 4 số dương a,b,c,d sao cho b=a+c/2 và c=2bd/b+d.CMR:a/b=c/d
3)Cho a,b,c là các số nguyên dương.CMR:M=a/a+b + b/b+c + c/c+a
Super Man mà lại còn phải lên đây để hỏi bài à?
Đúng 1
Bình luận (0)
1)Cho 1/c=1/2(1/a + 1/b) với a,b,c khác 0 và b khác c.CMR: a/b=a-c/c-b
2)Cho 4 số dương a,b,c,d sao cho b=a+c/2 và c=2bd/b+d.CMR:a/b=c/d
3)Cho a,b,c là các số nguyên dương.CMR:M=a/a+b + b/b+c + c/c+a
1)Cho 1/c=1/2(1/a + 1/b) với a,b,c khác 0 và b khác c.CMR: a/b=a-c/c-b
2)Cho 4 số dương a,b,c,d sao cho b=a+c/2 và c=2bd/b+d.CMR:a/b=c/d
3)Cho a,b,c là các số nguyên dương.CMR:M=a/a+b + b/b+c + c/c+a
Cho các số thực dương \(a;b;c;d\) thỏa mãn :\(a+b+c+d=4\). Chứng minh rằng :
\(\dfrac{1}{a^2+b+c+d}+\dfrac{1}{b^2+c+d+a}+\dfrac{1}{c^2+d+a+b}+\dfrac{1}{d^2+a+b+c}\le1\)
P/s: Em nhờ quý thầy cô giáo và các bạn hỗ trợ giúp đỡ với ạ!
Em cám ơn nhiều lắm ạ!
\(\left(a^2+b+c+d\right)\left(1+b+c+d\right)\ge\left(a+b+c+d\right)^2=16\)
\(\Rightarrow\dfrac{1}{a^2+b+c+d}\le\dfrac{1+b+c+d}{16}=\dfrac{5-a}{16}\)
Tương tự: \(\dfrac{1}{b^2+c+d+a}\le\dfrac{5-b}{16}\) ...
Cộng vế:
\(P\le\dfrac{20-\left(a+b+c+d\right)}{16}=1\)
Dấu "=" xảy ra khi \(a=b=c=d=1\)
Đúng 1
Bình luận (0)
Cho các số thực dương \(a;b;c;d\) thỏa mãn điều kiện \(a+b+c+d=4\). Chứng minh rằng
\(\dfrac{1}{a^2+b+c+d}+\dfrac{1}{b^2+c+d+a}+\dfrac{1}{c^2+d+a+b}+\dfrac{1}{d^2+a+b+c}\le1\)
P/s: Em xin phép quý thầy cô giáo và các bạn yêu toán, em nhờ mọi người vui lòng giúp đỡ em với ạ!
Em cám ơn nhiều lắm ạ!
Bunhiacopxki:
\(\left(a^2+b+c+d\right)\left(1+b+c+d\right)\ge\left(a+b+c+d\right)^2=16\)
\(\Rightarrow\dfrac{1}{a^2+b+c+d}\le\dfrac{1+b+c+d}{16}\)
Tương tự:
\(\dfrac{1}{b^2+c+d+a}\le\dfrac{1+c+d+a}{16}\) ; \(\dfrac{1}{c^2+d+a+b}\le\dfrac{1+d+a+b}{16}\)
\(\dfrac{1}{d^2+a+b+c}\le\dfrac{1+a+b+c}{16}\)
Cộng vế:
\(P\le\dfrac{4+3\left(a+b+c+d\right)}{16}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=d=1\)
Đúng 1
Bình luận (1)
cho các số dương a,b,c,d và có tích bằng 1.chứng minh :(a+b)(b+c)(c+d)(d+a)>=16
Cho a,b,c,d là các số nguyên dương,
a
≠
1
;
c
≠
1
thỏa mãn
log
a
b
3
2
,
log
c
d
5
4
và
a
-
c
9
. Khi đó
b
-
d
A.93 B.9 C.13 D.21
Đọc tiếp
Cho a,b,c,d là các số nguyên dương,
a ≠ 1 ; c ≠ 1 thỏa mãn log a b = 3 2 ,
log c d = 5 4 và a - c = 9 . Khi đó b - d
A.93
B.9
C.13
D.21