Bậc của đơn thức 13.x⁶.y.z⁴ ( dấu . là dấu ×)
NV
Những câu hỏi liên quan
cho các đơn thức sau , với a ,b là hằng số , x,y,z là biến số:
13.x(-2.x.y^2).(x.y^3.z^3);
1/2.a.x^2.y^2.(-1/3.a.b.x^3.y^2);
3.a.b.x.y.(-1/5.a.x^2.y.z).(-3.a.b.x^3.y.z^3)
a_thu gọn các đơn thức trên
b_xác định hệ số của mỗi đơn thức
c_xác định bậc của đơn thức đối với từng biến và đối với tập hợp các biến
Cho 4 đơn thức: x^3.y^2.z; 2.x^3.y.z^2; -3.x^2.y.z.t; x.y^2.z.t^3. Xác định dấu của x, y, z, t để 4 đơn thức:
a. Cùng dương
b. Cùng âm
\(\text{x^3.y^2.z (1)}\)
\(\text{2.x^3.y.z^2 (2)}\)
\(\text{-3.x^2.y.z.t (3)}\)
\(\text{x.y^2.z.t^3 (4)}\)
\(\text{a)Qua 2 đơn thức (1);(2) ta có :}\)
\(x.z>0\) (Để đơn thức là dương)
\(x.y>0\)(Để đơn thức là dương)
\(=>y.z>0\)
\(\text{Qua đơn thức (3) ta có :}\)
\(\text{t<0 (Để đơn thức là dương)}\)
\(=>t^3< 0\)
\(\text{Qua đơn thức (4) ta có :}\)
x.z<0 (Để đơn thức là dương)
Nhưng x.z > 0 (Theo biểu thức (1);(2)
=> Cả 4 đơn thức ko thể cùng dương
*phần b làm tương tự
*Bài này phông chữ bị lỗi phần cuối nên cố nhìn nhé --'
#ht
Cho hai đơn thức:(-6.x^2.y.z) và (2/3.x^2.y)
a, Tính tích của hai đơn thức
b, Tìm phần biến , bậc của tích trên
c, tính giá trị của (-6.x^2.y.z) tại x=-1; y=1/3 và z=-2
Cho hai đơn thức:(-6.x^2.y.z) và (2/3.x^2.y)
a, Tính tích của hai đơn thức
(-6.x^2.y.z) . (2/3.x^2.y)
= (-6.x^2.y.z) . (2/3.x^2.y)
= (-6.2/3).(x^2.x^2).(y.y).z
= -4. x^4. y^2 .z
b, Tìm phần biến , bậc của tích trên
Phần biến là -4
bậc của tích trên là : 4+2+1= 7
c, tính giá trị của (-6.x^2.y.z) tại x=-1; y=1/3 và z=-2
thay x=-1; y=1/3 và z=-2 vào (-6.x^2.y.z) ta có:
-6.\(\left(-1\right)^2.\dfrac{1}{3}.-2\)
=4
học tốt :D
Đúng 2
Bình luận (0)
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 2x + 1b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 4c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số a trong trường hợp Delta 0.
Đọc tiếp
a) Quan sát Hình 19 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 2x + 1\)
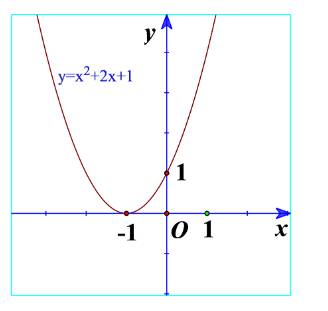
b) Quan sát Hình 20 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 4\)
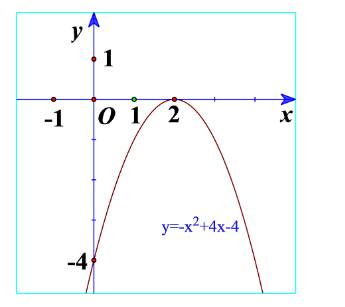
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta = 0\).
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
Đúng 0
Bình luận (0)
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} - 2x + 2b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 5c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số a trong trường hợp Delta 0.
Đọc tiếp
a) Quan sát Hình 17 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - 2x + 2\)
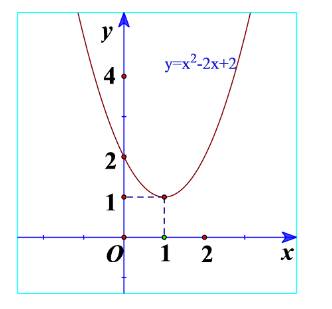
b) Quan sát Hình 18 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 5\)
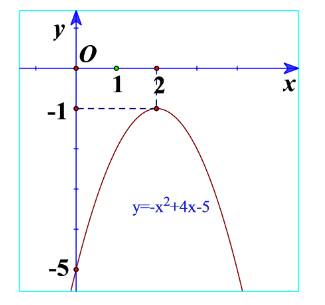
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số a trong trường hợp \(\Delta < 0\).
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
Đúng 0
Bình luận (0)
Thu gọn các đơn thức, chỉ rõ phần hệ số, phần biến, và tìm bậc của mỗi đơn thức. A= ( 2/3.X²y)².3/2 .x²y.z B= -2/3.xy².1/2.xy³ . -x²y² C= (4/3.x²y.-2/3.Xy³)².(x²y)³
a: \(A=\dfrac{4}{9}x^4y^2\cdot\dfrac{3}{2}x^2yz=\dfrac{2}{3}x^6y^3z\)
Hệ số; biến;bậc lần lượt là 2/3; x^6y^3z;10
b: \(B=\dfrac{-2}{3}\cdot\dfrac{1}{2}\cdot\left(-1\right)\cdot xy^2\cdot xy^3\cdot x^2y^2=\dfrac{1}{3}x^4y^7\)
Hệ số;biến;bậc lần lượt là 1/3;x^4y^7;11
c: \(C=\left(-\dfrac{8}{9}x^3y^4\right)^2\cdot x^6y^3=\dfrac{64}{81}x^6y^8\cdot x^6y^3=\dfrac{64}{81}x^{12}y^{11}\)
Hệ số;biến;bậc lần lượt là 64/81; x^12y^11; 23
Đúng 0
Bình luận (0)
dạ, cho em hỏi là tại sao khi xét tính đơn điệu của hàm bậc hai trên bậc nhất trên mỗi khoảng xác định, ta chỉ xét dấu của tam thức bậc hai mà không kèm theo điều kiện xác định của mẫu?
Cho bảng xét dấu:Bảng xét dấu trên là của tam thức bậc hai nào sau đây? A. f(x) -
x
2
- x + 6 B. f(x)
x
2
+ x - 6 C. f(x) -
x
2
+ x + 6 D. f(x)
x
2
- x + 6
Đọc tiếp
Cho bảng xét dấu:

Bảng xét dấu trên là của tam thức bậc hai nào sau đây?
A. f(x) = - x 2 - x + 6
B. f(x) = x 2 + x - 6
C. f(x) = - x 2 + x + 6
D. f(x) = x 2 - x + 6
Đáp án: A
Từ bảng xét dấu ta thấy phương trình f(x) = 0 có 2 nghiệm là -3 và 2. Do đó, ta loại được đáp án C và D
Dựa vào bảng xét dấu, f(x) > 0 trong khoảng (-3;2) do đó hệ số a < 0
Đúng 0
Bình luận (0)
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai fleft( x right) {x^2} + 3x + 2 tùy theo các khoảng của x.b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai fleft( x right) - {x^2} + 4x - 3 tùy theo các khoảng của x.c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai fleft( x right) a{x^2} + bx + cleft( {a ne 0} right) với dấu của hệ số tùy theo các khoảng của x trong trường hợp Delta 0.
Đọc tiếp
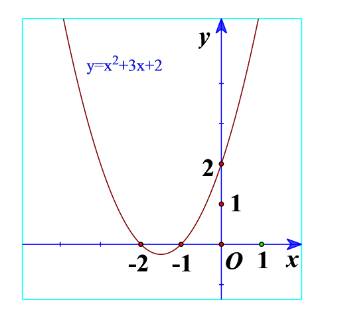
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = {x^2} + 3x + 2\) tùy theo các khoảng của x.
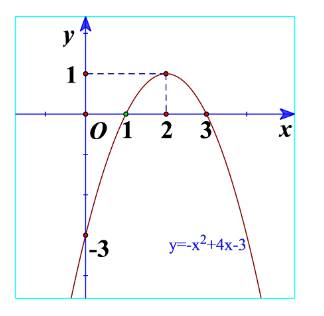
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai \(f\left( x \right) = - {x^2} + 4x - 3\) tùy theo các khoảng của x.
c) Từ đó rút ra mối liên hệ về dấu của tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) với dấu của hệ số tùy theo các khoảng của x trong trường hợp \(\Delta > 0\).
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
Đúng 0
Bình luận (0)



