Cho tam giác ABC vuông tại đỉnh B có AB = 12; BC = 9, có D là một điểm trên AB và E là một điểm trên AC, sao cho DE//BC. Biết AD = 4 cm. Tính độ dài ED; EC và AC Giúp mik với
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
WM
Những câu hỏi liên quan
cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Tính khoảng cách từ trọng tâm G của tam giác ABC tới các đỉnh A, B, C
Cho tam giác ABC cân tại A, hình vuông KLMN có đỉnh K trên cạnh AB, đỉnh L trên cạnh AC, các đỉnh M,N ở trên đáy BC
a) Tính tỉ số diện tích của tam giác và hình vuông khi tâm hình vuông trùng với trọng tâm tam giác
b) Tính cạnh hình vuông biết BC=16 ; AB=20
Cho tam giác ABC vuông tại đỉnh B có AB = 12; BC = 9, có D là một điểm trên AB và E là một điểm trên AC, sao cho DE//BC. Biết AD = 4 cm.Tính độ dài ED; EC và AC
Các bạn giúp mik phần ED; EC nhé !
Tinh AC ap dung dinh ly pi-ta-go
\(12^2+9^2=x^2\)
\(225=x^2\)
\(15=x\)
\(=>x=15\)
\(=>AC=15cm.\)
Đúng 0
Bình luận (0)
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
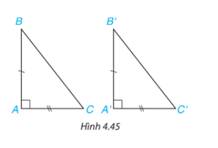
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Đúng 0
Bình luận (0)
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB AB, widehat B widehat {B} (H.4.46).Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Đọc tiếp
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
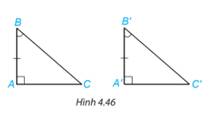
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=6cm; AC=8cm. Tính khoảng cách từ trọng tâm G của tam giác ABC tới các đỉnh A,B,C
Mong các bạn giúp đỡ
Câu 1. Tam giác ABC cân tại B có0 B 40 thì A bằng:A) 400 B) 700 C) 600 D) 500Câu 2. Tam giác AED có AD2 DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB EF, B F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC FD B) A F C) CE D) AECâu 4. Cho tam giác DEF vuông cân tại D, có DE3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cmII. BÀI TẬP TỰ LUẬN (8 điể...
Đọc tiếp
Câu 1. Tam giác ABC cân tại B có
0 B 40 thì A bằng:
A) 400 B) 70
0 C) 60
0 D) 50
0
Câu 2. Tam giác AED có AD2 = DE2 - AE2thì tam giác AEDA) vuông tại E B) vuông tại D C) vuông tại A D) không vuôngCâu 3. Cho tam giác ABC và tam giác có ba đỉnh D; E; F, biết AB = EF, B =F . Cần thêm điềukiện gì để hai tam giác bằng nhau theo trường hợp: góc - cạnh - góc?A) AC = FD B) A =F C) C=E D) A=ECâu 4. Cho tam giác DEF vuông cân tại D, có DE=3cm thì EF bằng:A) 18cm B) 12cm C) 12 cm D) 18 cm
II. BÀI TẬP TỰ LUẬN (8 điểm)Cho tam giác ABC có
0 A 90 và AB < BC. Gọi M là trung điểm của AC, trên tia đối của tia MB
lấy điểm D sao cho MD = MB. 1) Chứng minh ABM = CDM từ đó chứng minh AB=CD và AB //
Câu 1: B
Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)
=> Chọn A
Câu 3: Chọn D
Câu 4: \(EF=3\sqrt{2}cm\)
Đúng 1
Bình luận (0)
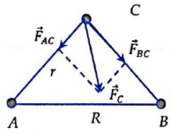
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền AB R. Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C. A.
3
5
G
m
2
R
2
B.
6
5
G
m
2
R...
Đọc tiếp
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền AB = R. Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C.
A. 3 5 G m 2 R 2
B. 6 5 G m 2 R 2
C. 12 G m 2 R 2
D. 6 G m 2 R 2
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền
A
B
R
. Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C. A.
3
5
G
m
2
R
2...
Đọc tiếp
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền A B = R . Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C.
A. 3 5 G m 2 R 2
B. 6 5 G m 2 R 2
C. 12 G m 2 R 2
D. 5 5 G m 2 R 2
Chọn B.
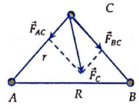
Vì tam giác ABC cân tại C nên ta có AC=BC= R 2
Lực hấp dẫn tác dụng lên chất điểm tại
![]()
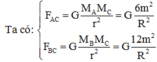
![]()
Đúng 0
Bình luận (0)