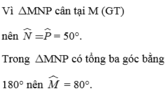Cho tam giác MNP cân tại M có M
PN
Những câu hỏi liên quan
cho tam giác MNP cân tại M có góc M = 2P. tính góc M,P,N. tam giác MNP là tam giác j. giúp mình với
góc P = 30 độ
góc M = 60 độ
ta áp dụng đl tổng 3 góc trog 1 tam giác
=> góc N = 90 độ
Vậy MNP là tam giác vuông cân .
Đúng 2
Bình luận (5)
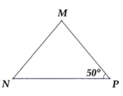
Cho tam giác MNP cân tại M có P ^ = 50 ° . Tính các góc còn lại của tam giác MNP.
Tam giác MNP có MN = NP và góc M bằng 45ᵒ, khi đó kết luận nào sau đây là đúng nhất?
Tam giác MNP vuông tại M
Tam giác MNP đều
Tam giác MNP cân tại N
Tam giác MNP vuông cân tại N
Tam giác MNP vuông cân tại N
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác MNP có góc M = 140°. Góc ngoài tại P có số đo 160°. Chứng minh rằng :
Tam giác MNP cân.
\(\widehat{MPN}\) \(=180^o-160^o=20^o.\)
Xét tam giác MNP:
\(\widehat{M}+\widehat{MPN}+\widehat{MNP}=\) \(180^o\) (Tổng 3 góc trong tam giác).
\(\Rightarrow140^o+20^o+\)\(\widehat{MNP}=\) \(180^o.\)
\(\Rightarrow\) \(\widehat{MNP}=20^{o}.\)
Xét tam giác MNP: \(\widehat{MPN}=\widehat{MNP} (=20^{o}).\)
\(\Rightarrow\) Tam giác MNP cân tại M.
Đúng 1
Bình luận (0)
Vì góc ngoài tại P có số đo là 160 độ nên ta có:
\(\widehat{M}+\widehat{N}=160^0\)
\(\Leftrightarrow\widehat{N}=20^0\)
\(\Leftrightarrow\widehat{P}=20^0\)
hay ΔMNP cân tại M
Đúng 1
Bình luận (0)
Cho tam giác MNP cân tại M có góc P = 50 độ. Tính các góc còn lại của tam giác MNP
Cho tam giác MNP cân tại M có góc P = 50 độ. Tính các góc còn lại của tam giác MNP
Giải
Vì \(\Delta MNP\)cân tại \(M\) \(\Rightarrow\widehat{N}=\widehat{P}\)mà \(\widehat{P}=50^o\left(gt\right)\Rightarrow\widehat{N}=50^o\)
Ta có \(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)
\(\Leftrightarrow\widehat{M}+50^o+50^o=180^o\)
\(\Leftrightarrow\widehat{M}+100^o=180^o\Rightarrow\widehat{M}=80^o\)
Vậy ............
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M có MN = 6 cm ,MP=8cm khi đó NP bằng:
a 🔼MNP vuông tại M b 🔼MNP vuông tại P
c 🔼MNP vuông tại N d 🔼MNP cân tại P
Xem thêm câu trả lời
Cho tam giác MNP cân tại M có M= 50o. Tính số đo góc N?
\(\widehat{N}=\dfrac{180^0-50^0}{2}=65^0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác MNP cân tại P có M ⏜ = 60 o . Khi đó
A. Tam giác MNP vuông cân tại P
B. Tam giác MNP vuông cân tại M
C. Tam giác MNP là tam giác đều
D. Tam giác MNP là tam giác vuông tại P
Ta có: tam giác MNP cân tại P có một góc M ⏜ = 60 o
Suy ra tam giác MNP đều (dấu hiệu nhận biết tam giác đều)
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
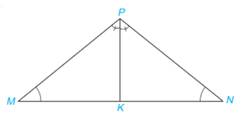
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Đúng 0
Bình luận (0)