Cho tam giác ABC có AB=6cm. Trên AC lấy điểm D sao cho AD=2/3 AC; trên BC lấy trung điểm I. Kéo dài DI cắt AB tại G. Tính độ dài của đoạn thẳng BG ?
CN
Những câu hỏi liên quan
cho tam giác abc có ab = 10cm ac = 15cm trên đường ab lấy điểm e sao cho ae = 6cm trên ac lấy điểm d sao cho ad= 4cm Chứng minh tam giác adb đồng dạng tam giác aec
Xét ΔADB và ΔAEC có
\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\left(\dfrac{4}{6}=\dfrac{10}{15}=\dfrac{2}{3}\right)\)
\(\widehat{A}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(c-g-c)
Đúng 0
Bình luận (0)
cho tam giác ABC có AB=6cm .Trên AC lấy điểm D sao cho AD=2/3 AC; trên BC lấy điểm K. Kéo dài ĐK cắt AB tại G .tính dộ dài của đoạn thẳng BG?
Cho tam giác ABC có góc A = 90 độ, AB=6cm , AC = 8 cm
a) tính BC
b) Trên cạnh AB lấy D sao cho AD = 2cm: trên tia đối của AC lấy E sao cho AC=AE. Chứng minh tam giác BDC = tam giác BDE
c) Gọi F là trung điểm của BE. Chứng minh 3 điểm C, D, F thẳng hàng
Cho tam giác ABC có AB=15cm ; AC=20cm . Trên cạnh AB lấy điểm D sao cho AD=8cm ; trên cạnh AC lấy E sao cho AE=6cm . Tính tỉ số diện tích của 2 tam giác AED và ABC
Xét tam giác AED Và Tam giác ABC có : Góc A chung và \(\frac{AE}{AB}=\frac{6}{15}=\frac{2}{5},\frac{AD}{AC}=\frac{8}{20}=\frac{2}{5}\) suy ra tam giác AED đồng dạng với tam giác ABC (cgc) suy ra \(S_{AED}:S_{ABC}=\left(\frac{AE}{AB}\right)^2=\left(\frac{2}{5}\right)^2=\frac{4}{25}\)
Đúng 1
Bình luận (1)
Cho tam giác ABc có AB=6cm; AC=7,5 , BC=9cm . Trên tia đối của tioa AB lấy điểm D sao cho AD=AC . Chứng minh tam giác ABC đồng dạng với tam giác CBD
( Khỏi vẽ hình )
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
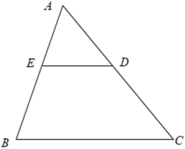
Xét Δ AED và Δ ABC có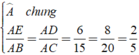
⇒ Δ AED ∼ Δ ABC ( c - g - c )
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 15 cm, AC = 20 cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD = 8cm, AE = 6cm. Chứng minh Δ AED ∼ Δ ABC.
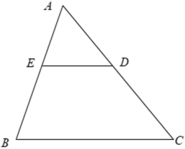
Xét Δ AED và Δ ABC có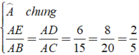
⇒ Δ AED ∼ Δ ABC ( c - g - c )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm .
a) Tính BC
b) Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC .
a: BC=10cm
b: Xét ΔEDB có
EA là đường cao
EA là đường trung tuyến
Do đó: ΔEDB cân tại E
Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCDB cân tại C
Xét ΔBEC và ΔDEC có
BE=DE
EC chung
BC=DC
Do đó: ΔBEC=ΔDEC
Đúng 1
Bình luận (0)
cho tam giác ABC có góc A= 90độ, AB=8cm, AC=6cm
a. Tính BC
b. Trên cạnh AC lấy điểm E sao cho AE=2cm, trên tia đối của tia AB lấy điểm D sao cho AD=AB. Chứng minh tam giác BEC= tam giác DEC



