Câu 4 ạ
TH
Những câu hỏi liên quan

Giups e câu câu 3 và câu 4 với ạ. Câu 4 e càn dàn ý thôi ạ
E cảm ơn nhiều ạ
Giúp mk câu 3 và câu 4 với ạ , mk cần gấp lắm ạ 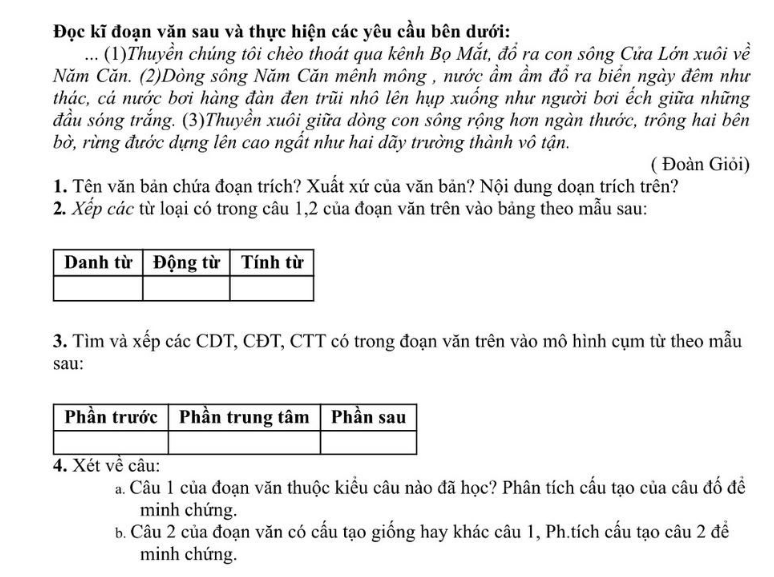
Mọi người giải giúp mình câu này ạ. Em cảm ơn. Câu 4 ạ
Xem chi tiết
Câu 4:
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
Giúp e làm các câu đó đi ạ trừ câu 3, 4 ra thôi ạ


 câu 4 thôi ạ, còn mấy câu khác mấy ac muốn lm hay k thì tùy ạ.
câu 4 thôi ạ, còn mấy câu khác mấy ac muốn lm hay k thì tùy ạ.
giúp mik vs ạ 4 câu ạ

câu 1 và câu 4 ạ

Câu 3,câu 4 thôi ạ
Chỉ em với ạ bỏ 1-4 ạ làm từ câu 5 ạ

5 since we last met our uncle
6 were pen pals 2 years ago
started being pen pals 2 years ago
7 not gone to London for 2 years
2 years since we last went to London
we went to London was 2 years ago
8 have never visited HN before
9 2 weeks since she last phoned home
10 seen his brother for nearly 20 years
11 seen our grandfather for 2 years
12 we went to the concert was a year ago
13 Linda talked to me was many years ago
14 we went to the beach was 10 years ago
15 taught English at this school since January 10th
16 I took photographs was 2 years ago
17 6 months since John last had his hair cut
18 we have seen this man here
19 never been to England before
20 the first time I have read a romantic story
21 she wrote to me was in March
22 taught the children in that remote village for 2 years
23 been married for 7 years
24 not written to me for years
Đúng 1
Bình luận (0)
 CÂU 4 CÂU 5 CÂU 6
CÂU 4 CÂU 5 CÂU 6
GIÚP MÌNH VỚI Ạ
Đổi: \(40\%=\dfrac{2}{5}\)
Số học sinh giỏi Anh bằng : \(1-\dfrac{3}{7}-\dfrac{2}{5}=\dfrac{6}{35}\) ( số học sinh trong câu lạc bộ )
Số học sinh trong câu lạc bộ là: \(48:\dfrac{6}{35}=280\) ( học sinh )
Số học sinh giỏi Toán là: \(280.\dfrac{3}{7}=120\) ( học sinh )
Số em giỏi Văn là: \(280-120-48=112\) ( học sinh )
Đúng 2
Bình luận (0)
Bài 4:
Số học sinh của câu lạc bộ là:
\(48:\left(1-\dfrac{3}{7}-\dfrac{2}{5}\right)=48:\dfrac{6}{35}=48\cdot\dfrac{35}{6}=280\)(bạn)
Số học sinh giỏi Toán là:
\(280\cdot\dfrac{3}{7}=120\)(bạn)
Số học sinh giỏi Văn là:
\(280\cdot\dfrac{2}{5}=112\)(bạn)
Đúng 1
Bình luận (0)
Câu 6:
Ta có
\(\dfrac{1}{1^2}=1;\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{50^2}< \dfrac{1}{49.50}\)
⇒ A \(=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{50^2}< \) \(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\)
⇒ A < \(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
⇒ A < \(1+\dfrac{99}{100}\)
⇒ A < \(1+\dfrac{99}{100}< 1+\dfrac{100}{100}\)
⇒ A < 2
Đúng 1
Bình luận (0)




