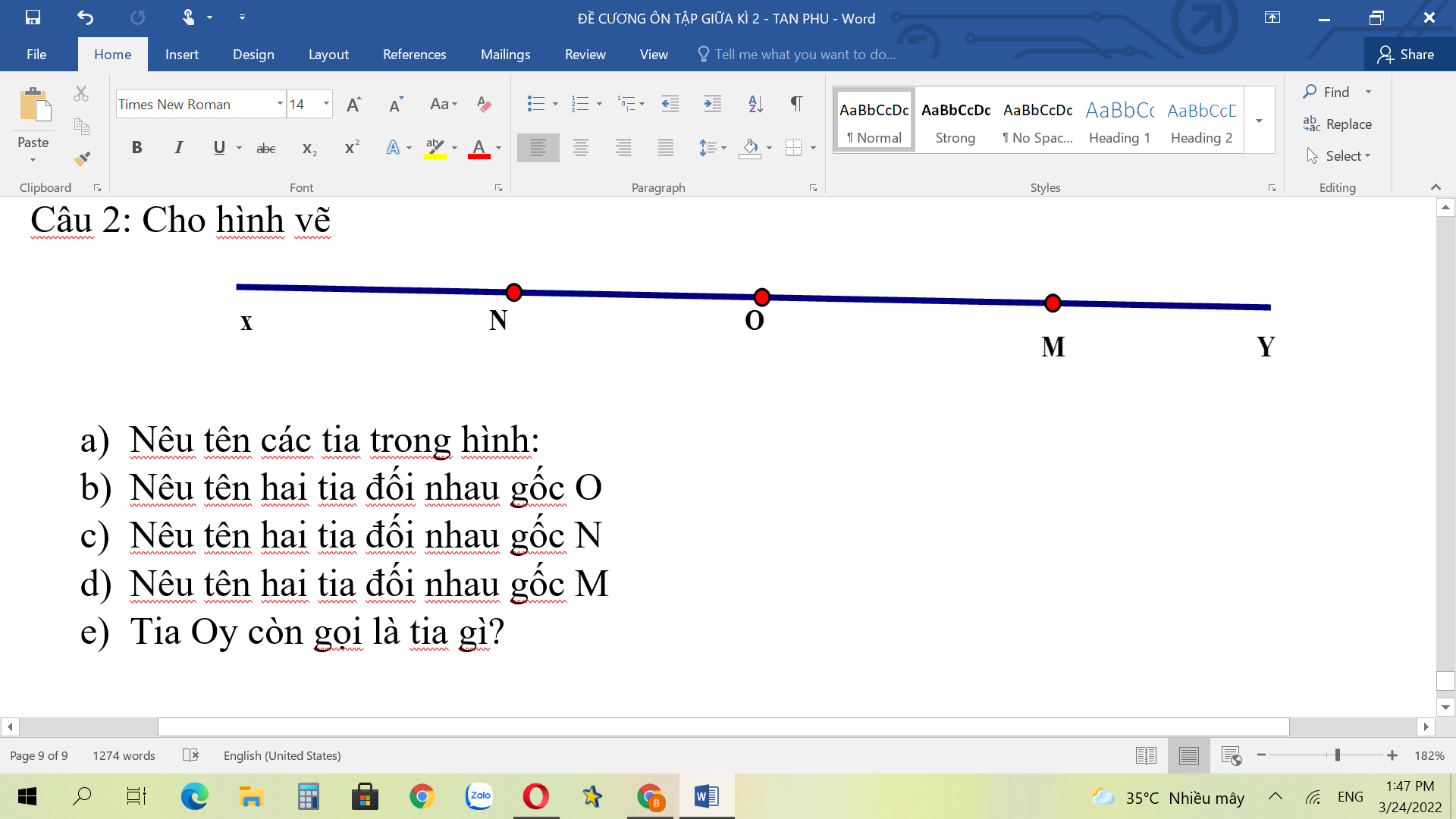
Giusp Mình với ạ ,mình cảm ơn nhiều
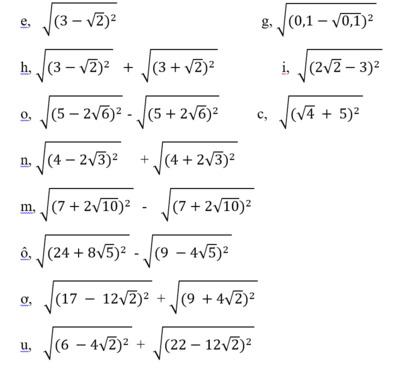
Thực hiện phép tính. Giusp mình nhanh với mng ạ@!!!! Mình cảm ơn nhiều.
e: \(=\left|3-\sqrt{2}\right|=3-\sqrt{2}\)
h: \(=3-\sqrt{2}+3+\sqrt{2}=6\)
g: \(=\left|0.1-\sqrt{0.1}\right|=0.1-\sqrt{0.1}\)
i: \(=\left|2\sqrt{2}-3\right|=3-2\sqrt{2}\)
c: \(=\left|2+5\right|=7\)
o: \(=5-2\sqrt{6}-5-2\sqrt{6}=-4\sqrt{6}\)
n: \(=4-2\sqrt{3}+4+2\sqrt{3}=8\)
m: \(=7+2\sqrt{10}-7-2\sqrt{10}=0\)
Giusp mình câu này đc ko ạ, mình cảm ơn rất nhiều:
Phân tích đa thức thành nhân tử: x^2-(5-y)^2
\(x^2-\left(5-y\right)^2\)
\(=[x+\left(5-y\right)].[x-\left(5-y\right)]\)
\(=\left(x+5-y\right).\left(x-5+y\right)\)
\(=\left(x-y+5\right).\left(x+y-5\right)\)
Giusp mình vs ạ, cảm ơn mn!
Giusp em bài này với mọi người ạ, em cảm ơn rất nhiều ạ.

a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)
Giusp em với mng oiq! em cảm ơn rất nhiều ạ!!
a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4
100 : 500 =
448 : 999 =
99:555=
Giusp mình với nhé cảm ơn mn nhiều

Giusp e câu 2 với ạ
E đg cần gấp ạ, e cảm ơn nhiều
2. Thành phần biệt lập phụ chú (Dấu gạch ngang em nhé!)
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp lắm ạ, làm nhanh hộ mình với <3
Cảm ơn lần nữa

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)