cho mình hỏi với:
tìm x:
x2 +5x+5=0
bài này giải theo cách lớp 8 nhé
Bài 1: Cho pt ẩn x:
x2 - 2(m + 1)x + m2 + 7 = 0 (1)
a) Giải pt (1) khi m = -1; m = 3.
b) Tìm m để pt (1) có nghiệm là 4. Tìm nghiệm còn lại.
c) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa:
* x12 + x22 = 0
* x1 - x2 = 0
Bài 2: Cho pt ẩn x:
x2 - 2x - m2 - 4 = 0 (1)
a) Giải pt (1) khi m = -2.
b) Tìm m để pt (1) có 2 nghiệm x1, x2 thỏa mãn:
* x12 + x22 = 20
* x13 + x23 = 56
* x1 - x2 = 10
Bài 1:
a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\
\Leftrightarrow x^2+1+7=0\\
\Leftrightarrow x^2+8=0\left(vô.lí\right)\)
Thay m=3 vào (1) ta có:
\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)
b, Thay x=4 vào (1) ta có:
\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)
c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)
\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)
Bài 2:
a,Thay m=-2 vào (1) ta có:
\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)
\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)
\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)
\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)
ai biết giải này thì giải giúp mình nhé,làm theo cách lớp 9 nhé ! Cảm ơn ạ.
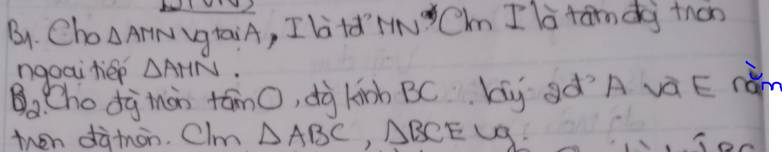
a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Ba lớp 6 có 102 HS. Số HS lớp A bằng 8/9 số HS lớp B, số HS lớp C bằng 17/16 số HS lớp A. Hỏi mỗi lớp có bao nhiêu HS?
Các bạn giải hộ mình với, giải theo cách bài giải nhé!
Gọi số học sinh của lớp 6A là a ; học sinh lớp 6B là b ; học sinh lớp 6C là c
Ta có : a = 8/9b (1)
c = 17/16a (2)
Thay (1) vào (2)
=> c = 17/16 . 8/9b
=> c = 17/18b (3)
Lại có a + b + c = 102
=> 8/9b + b + 17/18b = 102 (Theo (1) ; (3))
=> b(8/9 + 1 + 17/18) = 102
=> b.17/6 = 102
=> b = 36
=> a = 32
=> c = 34
Vậy số học sinh của lớp 6A là 32 em ; học sinh lớp 6B là 36 em ; học sinh lớp 6C là 34 em
Bài 1: Tìm 2 số biết rằng 9/11 số thứ nhất bằng 6/7 số thứ hai và tổng của chúng bằng 172
Giải bài này theo lời giải hộ mình nhé'! Đừng làm theo kiểu "gọi ..là x,.." nhé
Gọi số học sinh ba lớp A,B,C lần lượt là a,b,c(a,b,c>=0)
Theo đề bài ta có :
a=\(\frac{8}{9}b\):c=\(\frac{17}{16}a\)và a+b+c=102
a+b+c=8/9b+b+17/16(8/9b)=102
8/9b+b+17/18b=102
b(8/9+1+17/18)=102
b=102/(17/6)=36
a=8/9*36=32
c=17/16*32=34
Vậy số học sinh lớp A là 32
số học sinh lớp B là 36
số học sinh lớp C là 34
so sánh 37.37*5959.59 và 59.59*3737.37
các bạn giúp mình giải bài này nhé (nhớ giải theo cách học trên lớp nhé)
37.37 x 5959.59 = 222709.8783
59.59 x 3737.37 = 222709.8783
Vậy: điền dấu = nhé!
= nha chj
hai kết quả ra là 222709,8783 em nhá ^ ^
mình muốn làm theo cách học trên lớp để cho cô giáo chấm cơ
Giúp mình giải bài này với nhé
Tính theo cách thuận tiện nhất
4/3:5/4:6/5:7/6:8/7:9/8=
\(\frac{4}{3}:\frac{5}{4}:\frac{6}{5}:\frac{7}{6}:\frac{8}{7}:\frac{9}{8}\)
=\(\frac{4}{3}\times\frac{4}{5}\times\frac{5}{6}\times\frac{6}{7}\times\frac{7}{8}\times\frac{8}{9}\)
=\(\frac{16}{27}\)
Cho x, y, z là các số thực không âm. Cho k và m lần lượt là giá trị nhỏ nhất của \(\frac{x^2+y^2+z^2+1}{xy+yz+z}\) và \(\frac{x^2+y^2+z^2+1}{xy+y+z}\). Tính \(km+k+m\).
Các bạn trình bày cách giải đầy đủ hợp lí giúp mình nhé, mình đang cần kinh nghiệm để giải những bài như thế này. Mình mới học lớp 8 thôi, nên khuyến khích các bạn giải bằng cách lớp 8 hoặc lớp thấp hơn để mình có thể học hỏi nhé, cảm ơn:))
\(xy=\frac{1}{t}.txy\le\frac{t^2x^2+y^2}{2t}=\frac{\left(3+\sqrt{5}\right)x^2+y^2}{1+\sqrt{5}}\)\(t^2=\frac{3+\sqrt{5}}{2}\)
\(\frac{2\left(1+\sqrt{5}\right)\left(x^2+y^2+z^2+1\right)}{\left(3+\sqrt{5}\right)\left(2x^2+y^2+z^2+1\right)}\)
\(K=\frac{x^2+y^2+z^2+1}{xy+yz+z}=\frac{\left(1+\sqrt{5}\right)\left(x^2+y^2+z^2+1\right)}{2.\frac{1+\sqrt{5}}{2}x.y+\left(1+\sqrt{5}\right)yz+2.\frac{1+\sqrt{5}}{2}.z}\)
\(\ge\frac{\left(1+\sqrt{5}\right)\left(x^2+y^2+z^2+1\right)}{\frac{3+\sqrt{5}}{2}x^2+y^2+\frac{1+\sqrt{5}}{2}\left(y^2+z^2\right)+z^2+\frac{3+\sqrt{5}}{2}}=\frac{1+\sqrt{5}}{\frac{3+\sqrt{5}}{2}}=\sqrt{5}-1=k\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x=1\\y=\frac{1+\sqrt{5}}{2}\\z=\frac{1+\sqrt{5}}{2}\end{cases}}\)
\(M=\frac{x^2+y^2+z^2+1}{xy+y+z}=\frac{\left(\sqrt{5}-1\right)\left(x^2+y^2+z^2+1\right)}{2.x.\frac{\sqrt{5}-1}{2}y+\left(\sqrt{5}-1\right)y+2.\frac{\sqrt{5}-1}{2}.z}\)
\(\ge\frac{\left(\sqrt{5}-1\right)\left(x^2+y^2+z^2+1\right)}{x^2+\frac{3-\sqrt{5}}{2}y^2+\frac{\sqrt{5}-1}{2}\left(y^2+1\right)+\frac{3-\sqrt{5}}{2}+z^2}=\sqrt{5}-1=m\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x=\frac{-1+\sqrt{5}}{2}\\y=1\\z=\frac{-1+\sqrt{5}}{2}\end{cases}}\)
\(km+k+m=4\)
2 dòng đầu sai nhưng quên xoá :) bỏ đi nhé
Bây giờ là 3 giờ. Hỏi sau ít nhất là bao lâu nữa thì kim giờ và kim phút tạo tạo thành góc bẹt?
Các bạn giải theo cách lớp 5 giùm mình nhé! Ai nhanh mình tick cho!
Cho mình hỏi bài này với!!
Vẽ 10 đường thẳng cắt nhau tại 1 điểm O. Hỏi chúng tạo thành vao nhiêu góc??
Giải theo cách lớp 6 giúp mình với nha!!