vẽ hình hai góc cùng phụ với một góc thứ ba thì bằng nhau
HT
Những câu hỏi liên quan
vẽ hình ghi giả thiết ,kết luận :"hai góc cùng phụ với một góc thứ ba thì bằng nhau"
giả thiết:hai góc cùng phụ với một góc thứ ba
kết luận : thì bằng nhau
Đúng 0
Bình luận (0)
Ta gọi hai góc có tổng bằng $90^{\circ}$ là hai góc phụ nhau. Vẽ hình, viết giả thiết, kết luận bằng kí hiệu định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
Giả thiết - Kết luận:
| GT |
|
| KL |
Đúng 0
Bình luận (0)
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
Giả thiết - Kết luận:
| GT |
|
| KL | |
Đúng 1
Bình luận (0)
A
B
C
O
D
GT:DOA+AOB=90
AOB+BOC=90
KL:DOA=BOC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''.
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''.
Ta có : A1 + A2 = 90o
A3 + A2 = 90o
Mà A2 = A2
=> A1 = A3
Đúng 1
Bình luận (0)
Ta có: Góc xOy cộng góc yOz bằng 90 độ =>Góc xOy bằng 90 độ trừ số đo góc yOz
Góc zOt cộng góc yOz bằng 90 độ =>Góc zOt bằng 90 độ trừ số đo góc yOz
=>Góc xOy có số đo bằng góc zOt (cùng bằng 90 độ trừ số đo góc yOz)
Đúng 0
Bình luận (0)
ta co A2 +C = B+C (=90)
A2+C- C = B
=>A2=B
Đúng 0
Bình luận (0)
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''
| Giả thiết | \(\widehat{mOy}+\widehat{yOn}=90^0;\widehat{xOn}+\widehat{yOn}=90^0\) |
| Két luận | \(\widehat{mOy}=\widehat{xOn}\) |
C/m
Ta có
\(\widehat{mOy}+\widehat{yOn}=90^0;\widehat{xOn}+\widehat{yOn}=90^0\)
\(\Rightarrow\widehat{mOy}+\widehat{yOn}=\widehat{xOn}+\widehat{yOn}\)
\(\Rightarrow\widehat{mOy}+\widehat{yOn}-\widehat{yOn}=\widehat{xOn}+\widehat{yOn}-\widehat{yOn}\)
\(\Rightarrow\widehat{mOy}=\widehat{xOn}\) (đpcm)
Đúng 0
Bình luận (2)
Hình tự vẽ nha!!!!
gt:hai góc cùng phụ
kl:hai góc bằng nhau
giai : goi hai góc a va b cùng phụ với c ta dược
a+c=90 =>a=90-c
b+c=90=>b=90-c
từ 2 điều trên suy ra a=b
Đúng 0
Bình luận (2)
Chứng minh định lí: ''Hai góc cùng phụ với một góc thứ ba thì bằng nhau''.
Làm ơn ghi cách làm và vẽ hình.
Giả sử góc A và góc B cùng phụ với góc C => A + C = 900 , và B + C = 900.
=> A = 90 - C ; B = 90 - C
=> A = B
Đúng 0
Bình luận (0)
Vẽ hình họa, viết GT và KL của định lí :"Hai góc cùng bù với với một góc thứ ba thì hai góc đó bằng nhau".
| GT | \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau |
| KL | \(\widehat{CAB}=\widehat{GFE}\) |
Vì \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{CAB}=180^0\)
=>\(\widehat{CAB}=180^0-\widehat{CAD}\left(1\right)\)
Vì \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{GFE}=180^0\)
=>\(\widehat{GFE}=180^0-\widehat{CAD}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{CAB}=\widehat{GFE}\)
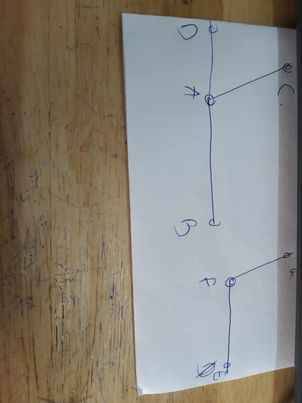
Đúng 0
Bình luận (0)
ghi giả thiết, kết luận, vẽ hình và chứng minh định lí:" Hai góc cùng phụ với một góc thứ ba thi bằng nhau "
Ghi giả thiết,kết luận và chứng minh :"Hai góc phụ nhau với góc thứ ba thì bằng nhau "
Ghi giả thiết,kết luận và chứng minh:"Hai góc cùng bù với một góc thứ ba thì bằng nhau".




