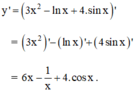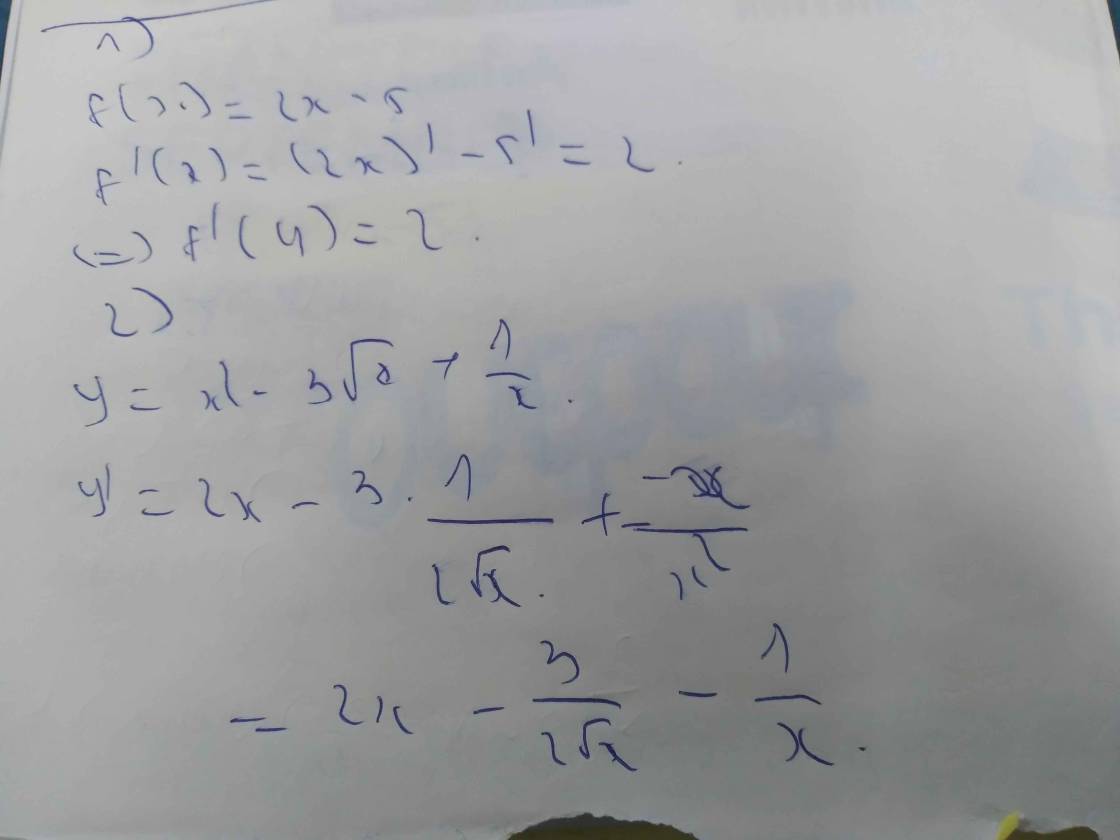tính đạo hàm của hàm số sau: (3x2+4).\(\sqrt{x}\)
NV
Những câu hỏi liên quan
Tính đạo hàm của hàm số sau: y=\(\sqrt{4-x}+\sqrt{4+x}\) tại \(y'\ge0\)
Lời giải:
Đạo hàm \(y'=\frac{-1}{2\sqrt{4-x}}+\frac{1}{2\sqrt{4+x}}\)
Đoạn tìm đạo hàm tại $y'\geq 0$ ý bạn là gì nhỉ?
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau: y = 3 x 2 - 2 log 2 x
Tính đạo hàm của các hàm số sau: y = 1 2 + 3 x 2
Tính đạo hàm của hàm số sau:
y
(
2
x
3
-
3
x
2
+
6
x
+
1
)
2
A.
2
2
x
3
-
x
2
+
6
x
+
1...
Đọc tiếp
Tính đạo hàm của hàm số sau: y = ( 2 x 3 - 3 x 2 + 6 x + 1 ) 2
A. 2 2 x 3 - x 2 + 6 x + 1 6 x 2 - 6 x + 6
B. 2 2 x 3 - 3 x 2 + x + 1 x 2 - 6 x + 6
C. 2 2 x 3 - 3 x 2 + 6 x + 1 x 2 - 6 x + 6
D. 2 2 x 3 - 3 x 2 + 6 x + 1 6 x 2 - 6 x + 6
- Sử dụng công thức ( u α ) ' với
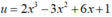 .
.
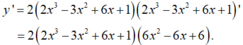
Chọn D.
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau:
y
(
9
−
2
x
)
(
3
x
2
−
3
x
+
1
)
A.
−
18
x
2
+
46
x
−
21
B.
−
10
x
2
+
66...
Đọc tiếp
Tính đạo hàm của hàm số sau: y = ( 9 − 2 x ) ( 3 x 2 − 3 x + 1 )
A. − 18 x 2 + 46 x − 21
B. − 10 x 2 + 66 x − 19
C. − 18 x 2 + 66 x − 29
D. − 12 x 2 + 48 x − 21
y ' = 9 - 2 x 3 x 2 - 3 x + 1 ' = ( 9 − 2 x ) ' . ( 3 x 2 − 3 x + 1 ) + ( 3 x 2 − 3 x + 1 ) ' . ( 9 − 2 x ) = − 2 ( 3 x 2 − 3 x + 1 ) + ( 6 x − 3 ) ( 9 − 2 x )
= − 6 x 2 + 6 x − 2 + 54 x − 12 x 2 − 27 + 6 x = − 18 x 2 + 66 x − 29
Chọn đáp án C
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau: y (2x3 – 3x2 – 6x + 1)2. A. 2(2x3 – x2 + 6x + 1)(6x2 – 6x + 6) B. 2(2x3 - 3x2 + x + 1)(x2 – 6x + 6) C. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6) D. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
Đọc tiếp
Tính đạo hàm của hàm số sau: y = (2x3 – 3x2 – 6x + 1)2.
A. 2(2x3 – x2 + 6x + 1)(6x2 – 6x + 6)
B. 2(2x3 - 3x2 + x + 1)(x2 – 6x + 6)
C. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
D. 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6)
Chọn D.
Sử dụng công thức đạo hàm của hàm hợp ![]() với u = 2x3 – 6x + 1
với u = 2x3 – 6x + 1
y' = 2(2x3 – 3x2 + 6x + 1)(2x3 – 3x2 + 6x + 1)’ = 2(2x3 – 3x2 + 6x + 1)(6x2 – 6x + 6).
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số
y = 3 x 2 - ln x + 4 . sin x
Đạo hàm của hàm số
y
x
2
+
x
+
3
x
2
+
x
−
1
bằng biểu thức nào sau đây? A.
−
2
(
2
x...
Đọc tiếp
Đạo hàm của hàm số y = x 2 + x + 3 x 2 + x − 1 bằng biểu thức nào sau đây?
A. − 2 ( 2 x + 1 ) x 2 + x − 1 2
B. − 4 ( 2 x + 1 ) x 2 + x − 1 2
C. − 4 ( 2 x − 1 ) x 2 + x − 1 2
D. − 4 ( 2 x + 4 ) x 2 + x − 1 2
Áp dụng công thức u v ' = u ' . v − v ' . u v 2 .
Ta có:
y ' = x 2 + x + 3 ' x 2 + x − 1 − x 2 + x − 1 ' x 2 + x + 3 x 2 + x − 1 2
= ( 2 x + 1 ) ( x 2 + x − 1 ) − ( 2 x + 1 ) . ( x 2 + x + 3 ) ( x 2 + x − 1 ) 2 = ( 2 x + 1 ) . ( x 2 + x − 1 − x 2 − x − 3 ) ( x 2 + x − 1 ) 2 = − 4 2 x + 1 x 2 + x − 1 2
Chọn đáp án B
Đúng 0
Bình luận (0)
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Đúng 3
Bình luận (0)