cho f(x)+g(x)=x2+1 và g(x)-f(x)=2x.Tìm đa thức f(x) và g(x)
NL
Những câu hỏi liên quan
Cho các đa thức f(x) = x5 – 3x2 + x3 – x2 - 2x + 5
g(x) = x5 – x4 + x2 - 3x + x2 + 1
a) Thu gọn và sắp xếp đa thức f(x) và g(x) theo luỹ thừa giảm dần.
b)Tính h(x) = f(x) + g(x)
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
Đúng 1
Bình luận (0)
Cho hai đa thức:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
Tính f(x) + g(x) và f(x) – g(x)
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
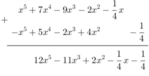
* f(x) - g(x)
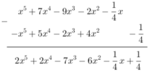
Đúng 0
Bình luận (0)
Cho hai đa thức f(x)=x2 + 3x - 5 và g(x) = x2 + 2x + 3
a) Tính f (x) + g (x)
b) Tính f(x)-g(x)
`a)f(x)+g(x)`
`=x^2+3x-5+x^2+2x+3`
`=(x^2+x^2)+(3x+2x)+(3-5)`
`=2x^2+5x-2`
`b)f(x)-g(x)`
`=x^2+3x-5-(x^2+2x+3)`
`=(x^2-x^2)+(3x-2x)-(3+5)`
`=x-8`
Đúng 2
Bình luận (0)
Cho đa thức f (x) = ax+b và g (x) = cx+d . Chứng minh nếu có hai giá trị x1 và x2 của x mà x1 khác x2 sao cho f (x1) = g (x1) và f (x2) = g (x2) thì f (x) = g (x) với mọi x thuộc Z
Cho đa thức f (x) = ax+b và g (x) = cx+d . Chứng minh nếu có hai giá trị x1 và x2 của x mà x1 khác x2 sao cho f (x1) = g (x1) và f (x2) = g (x2) thì f (x) = g (x) với mọi x thuộc Z
Cho đa thức
f
(
x
)
x
2
-
(
m
-
1
)
x
+
3
m
-
2
và
g
(
x
)
x
2
-
2
(
m
+
1
)
x
-
5
m
...
Đọc tiếp
Cho đa thức f ( x ) = x 2 - ( m - 1 ) x + 3 m - 2 và
g ( x ) = x 2 - 2 ( m + 1 ) x - 5 m + 1 . Tìm m biết f(1) = g(2)
A. a = 9 10
B. a = 3 10
C. a = 1 10
D a = - 1 10
Ta có f(1) = 12 -(m - 1).1 + 3m - 2 = 2m
g(2) = 22 - 2(m + 1).2 - 5m + 1 = -9m + 1
Vì f(1) = g(2) ⇒ 2m = -9m + 1 ⇒ 11m = 1 ⇒ m = 1/11. Chọn D
Đúng 0
Bình luận (0)
Cho hai đa thức
f
(
x
)
-
x
2
-
2
x
-
1
,
g
(
x
)
x
2
+
3
x
-
1
. Tìm nghiệm cúa đa thức
f
(
x
)
+
g
(
x
)
là: A. x -2 B. x -1...
Đọc tiếp
Cho hai đa thức f ( x ) = - x 2 - 2 x - 1 , g ( x ) = x 2 + 3 x - 1 . Tìm nghiệm cúa đa thức f ( x ) + g ( x ) là:
A. x = -2
B. x = -1
C. x = 1
D. x = 2
Ta có: f(x) + g(x) = x - 2. Cho x - 2 = 0 ⇒ x = 2. Chọn D
Đúng 0
Bình luận (0)
bài 11: cho đa thức F(x)=-x+2+5x2+2x4+2x3+x2+x4
G(x)=-x2+x3+x-6-3x3-4x2-3x4
a. thu gọn các đa thức trên theo thu gọn phổ biến
b.Tính F(x)+G(x);F(x)-G(x)
c. tìm nghiệm của đa thức F(x)+G(x)
a: f(x)=3x^4+2x^3+6x^2-x+2
g(x)=-3x^4-2x^3-5x^2+x-6
b: H(x)=f(x)+g(x)
=3x^4+2x^3+6x^2-x+2-3x^4-2x^3-5x^2+x-6
=x^2-4
f(x)-g(x)
=3x^4+2x^3+6x^2-x+2+3x^4+2x^3+5x^2-x+6
=6x^4+4x^3+11x^2-2x+8
c: H(x)=0
=>x^2-4=0
=>x=2 hoặc x=-2
Đúng 0
Bình luận (0)
Cho đa thức f(x)
x
4
–
3
x
3
+
3
x
2
+ ax + b và đa thức g(x)
x
2
– 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng A. -12 B. 12 C. -6 D. -8
Đọc tiếp
Cho đa thức f(x) = x 4 – 3 x 3 + 3 x 2 + ax + b và đa thức g(x) = x 2 – 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng
A. -12
B. 12
C. -6
D. -8
Ta có
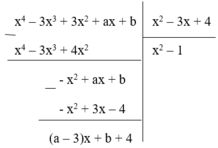
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)




