Giúp mình bài 9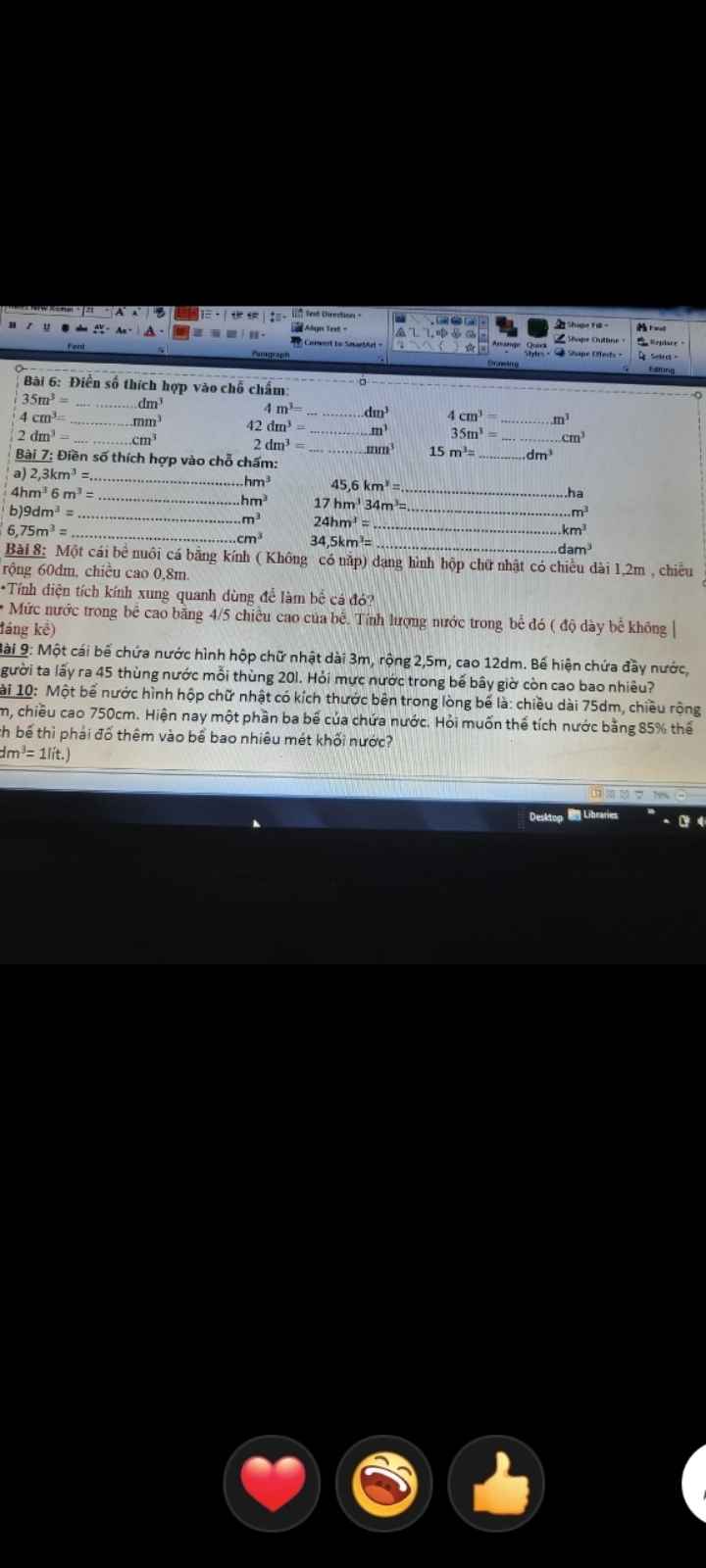
HP
Những câu hỏi liên quan
 mình không biết bài 9 bài 10 giúp mình với ạ !
mình không biết bài 9 bài 10 giúp mình với ạ !
Xem thêm câu trả lời
Giải giúp mình bài tập 67 ,68 ,69 bài 9 căn bậc ba nha tại mình bị mất sách rồi giúp mình
bài 69 Hãy tính (SGK)
1/ \(\sqrt[3]{512}=8\)
2/ \(\sqrt[3]{-729}=-9\)
3/ \(\sqrt[3]{0,064}=0,4\)
4/ \(\sqrt[3]{-0,216}=0,6\)
5/ \(\sqrt[3]{-0,008}=-0,2\)
Bài 68 Tính
1/ \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\)
=\(\sqrt[3]{3^3}-\sqrt[3]{-2^3}-\sqrt[3]{-5^3}\)
=\(3+2-5=0\)
2/ \(\frac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}\)
=\(\frac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{216}\)
=\(\sqrt[3]{27}-\sqrt[3]{6^3}=3-6=-3\)
Bài 69 So sánh
1/ 5 và \(\sqrt[3]{123}\)
ta có: \(5=\sqrt[3]{125}\)
\(125>123\)
Nên \(\sqrt[3]{125}>\sqrt[3]{123}\)
Vậy \(5>\sqrt[3]{123}\)
2/\(5\sqrt[3]{6}\) và \(6\sqrt[3]{5}\)
ta có: \(5\sqrt[3]{6}=\sqrt[3]{750}\)
\(6\sqrt[3]{5}=\sqrt[3]{1080}\)
=> 750 < 1080
Nên \(\sqrt[3]{750}< \sqrt[3]{1080}\)
Vậy \(5\sqrt[3]{6}< 6\sqrt[3]{5}\)
Đúng 0
Bình luận (0)
Giúp mình bài này vs ạ bài 9 nhá
anh rất tiếc lần sau hỏi che chữ kiểm tra đi nhé
Đúng 2
Bình luận (5)
 Giúp mình bài 9 ạ. Nhanh dùm mình nhé
Giúp mình bài 9 ạ. Nhanh dùm mình nhé
- Bầu trời cao xanh vời vợi còn gió dịu dàng tinh nghịch chơi đùa cùng mây.
=> Cách nối sử dụng từ ngữ có tác dụng nối
- Sáng ra hoa quỳnh đã tàn mà hương hoa vẫn chưa tan.
=> Cách nối sử dụng từ ngữ có tác dụng nối
- Bà kể chuyện say sưa bao nhiêu, chúng tôi càng bị lôi cuốn với lời kể của bà bấy nhiêu
=> Cách nối: quan hệ từ bao nhiêu - bấy nhiêu
- Do nó chủ quan nên chiếc xe đạp đã bị mất cắp.
=> Cách nối: quan hệ từ do - nên
Đúng 3
Bình luận (0)
 giúp mình bài 9
giúp mình bài 9
 mng giúp mình bài 9 với ạ
mng giúp mình bài 9 với ạ
Giúp mình làm từ bài 9 đến bài 16 với


9.
\(\Leftrightarrow a^2+a^2b^2+b^2+b^2c^2+c^2+c^2a^2\ge6abc\)
\(\Leftrightarrow\left(a^2-2abc+b^2c^2\right)+\left(b^2-2abc+c^2a^2\right)+\left(c^2-2abc+a^2b^2\right)\ge0\)
\(\Leftrightarrow\left(a-bc\right)^2+\left(b-ca\right)^2+\left(c-ab\right)^2\ge0\) (luôn đúng)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;0;0\right);\left(1;1;1\right);\left(1;-1;-1\right)\) và các hoán vị
10.
\(a^2+b^2+c^2=1\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=1+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow\left(a+b+c\right)^2=1+2\left(ab+bc+ca\right)\)
\(\Rightarrow1+2\left(ab+bc+ca\right)\ge0\Rightarrow ab+bc+ca\ge-\dfrac{1}{2}\)
Lại có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow ab+bc+ca\le1\)
Đúng 2
Bình luận (0)
11.
Do \(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\)
Do đó:
\(abc+2\left(1+a+b+c+ab+bc+ca\right)\)
\(=1+a+b+c+ab+bc+ca+\left(1+a+b+c+ab+bc+ca+abc\right)\)
\(=\dfrac{1}{2}\left(a^2+b^2+c^2\right)+ab+bc+ca+a+b+c+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(=\dfrac{1}{2}\left(a+b+c\right)^2+\left(a+b+c\right)+\dfrac{1}{2}+\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(=\dfrac{1}{2}\left(a+b+c+1\right)^2+\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge0\) (đpcm)
Đúng 1
Bình luận (0)
12.
\(a^4+3\ge4a\)
\(\Leftrightarrow a^4-2a^3+a^2+\left(2a^3-4a^2+2a\right)+\left(3a^2-6a+3\right)\ge0\)
\(\Leftrightarrow a^2\left(a-1\right)^2+2a\left(a-1\right)^2+3\left(a-1\right)^2\ge0\)
\(\Leftrightarrow\left(a^2+2a+3\right)\left(a-1\right)^2\ge0\)
\(\Leftrightarrow\left[\left(a+1\right)^2+2\right]\left(a-1\right)^2\ge0\) (luôn đúng)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
giúp mình từ bài 3 đến bài 9 là được
Giúp mình bài 2c, bài 3, 7b, 8, 9, 10 Các bạn làm được càng nhiều càng tốt không thì ít nhất một câu giúp mình!!

Bài 10:
\(\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\left(a\ne b\ne c\right)\\ \Leftrightarrow\left(a+b\right)\left(c-a\right)=\left(c+a\right)\left(a-b\right)\\ \Leftrightarrow ac-a^2+bc-ab=ac-bc+a^2-ab\\ \Leftrightarrow2a^2=2bc\\ \Leftrightarrow a^2=bc\)
Đúng 0
Bình luận (2)



