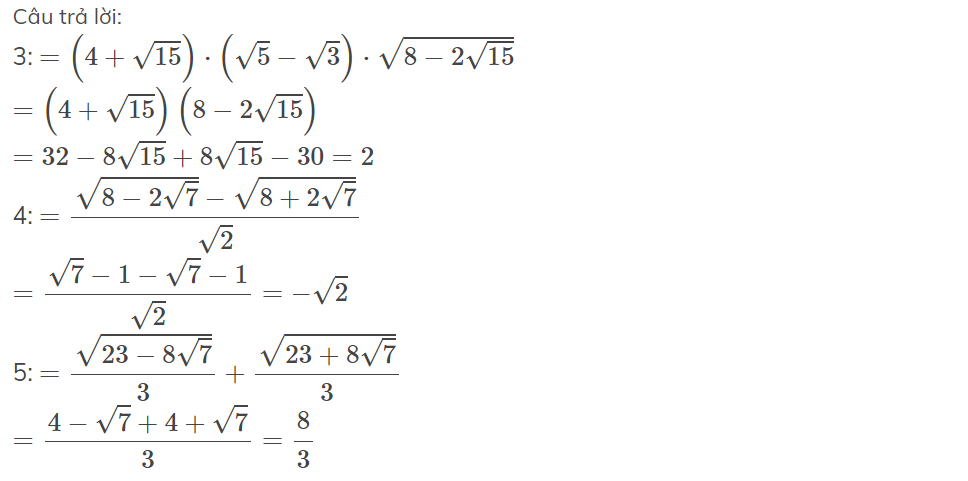GPT : \(\sqrt{2\cdot x^2-15\cdot x+26}=x-4\)
LN
Những câu hỏi liên quan
GPT : x = \(\sqrt{2-x}\cdot\sqrt{3-x}+\sqrt{3-x}\cdot\sqrt{5-x}+\sqrt{5-x}\cdot\sqrt{2-x}\)
\(\frac{2\cdot x^4-5\cdot x^3+2\cdot x^2-5\cdot x-30}{x^2+10\cdot x-15}\) với x=\(-\sqrt{5}\)
Giải các phương trình sau
a) -x^2+4cdot x+12cdotsqrt{2cdot x+1}
b) x+sqrt{x+dfrac{1}{2}+sqrt{x+dfrac{1}{4}}}2
c) 5cdot x^2-2cdot x+1left(4cdot x-1right)cdotsqrt{x^2+1}
d) left(2cdot x-1right)cdotsqrt{10-4cdot x^2}5-2cdot x
e) sqrt{2cdot x-1}-sqrt{x+1}2cdot x-4
f) sqrt{x^2-2cdot x}+sqrt{2cdot x^2+4cdot x}2cdot x
Đọc tiếp
Giải các phương trình sau
a) \(-x^2+4\cdot x+1=2\cdot\sqrt{2\cdot x+1}\)
b) \(x+\sqrt{x+\dfrac{1}{2}+\sqrt{x+\dfrac{1}{4}}}=2\)
c) \(5\cdot x^2-2\cdot x+1=\left(4\cdot x-1\right)\cdot\sqrt{x^2+1}\)
d) \(\left(2\cdot x-1\right)\cdot\sqrt{10-4\cdot x^2}=5-2\cdot x\)
e) \(\sqrt{2\cdot x-1}-\sqrt{x+1}=2\cdot x-4\)
f) \(\sqrt{x^2-2\cdot x}+\sqrt{2\cdot x^2+4\cdot x}=2\cdot x\)
câu b đk x>= -1/4
\(x+\sqrt{x+\dfrac{1}{2}+\sqrt{x+\dfrac{1}{4}}}=2\)
\(x+\sqrt{\left(\sqrt{x+\dfrac{1}{4}}+\dfrac{1}{2}\right)^2}=2\)
\(\left(\sqrt{x+\dfrac{1}{4}}+\dfrac{1}{2}\right)^2=2\)
\(x+\dfrac{1}{4}=\left(\sqrt{2}-\dfrac{1}{2}\right)^2\)
\(x=\left(\sqrt{2}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)
\(x=\left(\sqrt{2}-\dfrac{1}{2}-\dfrac{1}{2}\right)\left(\sqrt{2}-\dfrac{1}{2}+\dfrac{1}{2}\right)\)
\(x=\sqrt{2}\left(\sqrt{2}-1\right)=2-\sqrt{2}\)
Đúng 0
Bình luận (3)
\(\sqrt{2\cdot x^2+4\cdot x+6}\) +\(\sqrt{3\cdot x^2+6\cdot x+12}\)=5-\(2\cdot x\)-\(x^2\)
tìm Min F biết F=\(\frac{4\cdot\sqrt{x}+15}{2\cdot\sqrt{x}+9}\)
\(F=\frac{4.\sqrt{x}+15}{2.\sqrt{x}+9}=\frac{4.\sqrt{x}+18-3}{2.\sqrt{x}+9}=\frac{2.\left(2.\sqrt{x}+9\right)}{2.\sqrt{x}+9}-\frac{3}{2.\sqrt{x}+9}=2-\frac{3}{2.\sqrt{x}+9}\)
Có: \(2.\sqrt{x}+9\ge9\Rightarrow\frac{3}{2.\sqrt{x}+9}\le\frac{1}{3}\)
\(\Rightarrow F=2-\frac{3}{2.\sqrt{x}+9}\ge\frac{5}{3}\)
Dấu "=" xảy ra khi \(2.\sqrt{x}=0\Rightarrow\sqrt{x}=0\Rightarrow x=0\)
Vậy Min F = \(\frac{5}{3}\)khi x = 0
Đúng 0
Bình luận (0)
để tìm \(min\) của \(F\) ta xét \(GTNN\)của\(\sqrt{x}\)
\(GTNN\)của \(\sqrt{x}\)là \(0\)
thay \(0\)vào căn của biểu thức ta có:
\(F=\frac{4.\sqrt{0}+15}{2.\sqrt{0}+9}=\frac{15}{9}\approx1,6666666666667\)
vậy \(min\)của \(F\)\(\approx1,6\)
Đúng 0
Bình luận (0)
Tính
1, a = \(\sqrt[3]{45+26\sqrt{2}}+\sqrt[3]{45-29\sqrt{2}}\)
2, x = \(\sqrt[3]{4+\sqrt{80}-\sqrt[3]{\sqrt{80}-4}}\)
3, \(\left(4+\sqrt{15}\right)\cdot\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4-\sqrt{15}}\)
4, \(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)
5, \(\sqrt{\frac{4-\sqrt{7}}{4+\sqrt{7}}}+\sqrt{\frac{4+\sqrt{7}}{4-\sqrt{7}}}\)
GPT: \(x^2-\frac{\sqrt{5}}{\sqrt{5}-2}\cdot x-\left(6-2\sqrt{5}\right)=0\)
giải hệ phương trình :
a) \(\hept{\begin{cases}x\cdot\left(1+y-x\right)=-2\cdot y^2-y\\x\cdot\left(\sqrt{2\cdot y}-2\right)=y\cdot\left(\sqrt{x-1}-2\right)\end{cases}}\)
b) \(\hept{\begin{cases}1+x\cdot y+\sqrt{x\cdot y}=x\\\frac{1}{x\cdot\sqrt{x}}+y\cdot\sqrt{y}=\frac{1}{\sqrt{x}}+3\cdot\sqrt{y}\end{cases}}\)
Làm hộ mk nhé mk tick cho :))))))))))
Giải phương trình:a)sqrt[3]{14-x^3}+x2cdotleft(1+sqrt{x^2-2x-1}right)b) 5-3xleft(-125x^2+150x-41right)cdotsqrt{1-x^2}c)sqrt{2x^2+1}+sqrt{x^2+3x+2}sqrt{x^2-x+4}+sqrt{2x^2+2x+3}d) sqrt{x^2+15}+2sqrt{x^2+8}+3xe) sqrt{2x^4+2}cdotleft(sqrt{2-x}-sqrt{x}right)left(1-xright)cdotleft(x^2+1right)f) sqrt[3]{2037-x}-sqrt{x-2009}x^2-2009x-2008
Đọc tiếp
Giải phương trình:
a)\(\sqrt[3]{14-x^3}+x=2\cdot\left(1+\sqrt{x^2-2x-1}\right)\)
b) \(5-3x=\left(-125x^2+150x-41\right)\cdot\sqrt{1-x^2}\)
c)\(\sqrt{2x^2+1}+\sqrt{x^2+3x+2}=\sqrt{x^2-x+4}+\sqrt{2x^2+2x+3}\)
d) \(\sqrt{x^2+15}+2=\sqrt{x^2+8}+3x\)
e) \(\sqrt{2x^4+2}\cdot\left(\sqrt{2-x}-\sqrt{x}\right)=\left(1-x\right)\cdot\left(x^2+1\right)\)
f) \(\sqrt[3]{2037-x}-\sqrt{x-2009}=x^2-2009x-2008\)
giải bài nào hộ mk cx được ko cần lm hết đâu :) :) :)
Đúng 0
Bình luận (0)