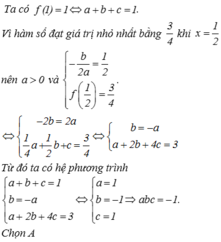Cho a + b , 2a và x là các số nguyên . Chứng minh y =\(ax^2+bx+2013\) nhận giá trị nguyên
DM
Những câu hỏi liên quan
Cho f(x)= ax3+bx2+cx+d. Chứng minh rằng f(x) nhận được giá trị nguyên với mọi x thuộc Z khi và chỉ khi 6a;2b;a+b+c và d là số nguyên.
a) Cho đa thức f(x)= ax2+bx+c với a,b,c là các số thực. Biết rằng f(0) ; f(1) ; f(2) có trị nguyên. Chứng minh rằng 2a,2b,2c có giá trị nguyên.
c) Tìm x,y thuộc N biết : 36-y2=8.(x-2010)2
\(f\left(x\right)=ax^2+bx+c\Rightarrow\hept{\begin{cases}f\left(0\right)=c\\f\left(1\right)=a+b+c\\f\left(2\right)=4a+2b+c\end{cases}}\)
\(f\left(0\right)\) nguyên \(\Rightarrow c\) nguyên \(\Rightarrow\hept{\begin{cases}2a+2b\\4a+2b\end{cases}}\) nguyên
\(\Rightarrow\left(4a+2b\right)-\left(2a+2b\right)=2a\)(nguyên)
\(\Rightarrow2b\) nguyên
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
\(36-y^2\le36\)
\(8\left(x-2010\right)^2\ge0;8\left(x-2010\right)^2⋮8\)
\(\Rightarrow\hept{\begin{cases}0\le8\left(x-2010\right)^2\le36\\8\left(x-2010\right)^2⋮8\\8\left(x-2010\right)^2\in N\end{cases}}\)
Giai tiep nhe
Đúng 0
Bình luận (0)
Cho a và b là các số nguyên dương
lim
x
→
0
a
a
x
-
1
sin
b
x
5
3
Tích có thể nhận giá trị bằng số nào trong các số dưới đây? A. 15. B. 60. C. 240. D. Cả ba đáp án trên.
Đọc tiếp
Cho a và b là các số nguyên dương lim x → 0 a a x - 1 sin b x = 5 3 Tích có thể nhận giá trị bằng số nào trong các số dưới đây?
A. 15.
B. 60.
C. 240.
D. Cả ba đáp án trên.
Chọn D.
Ta có 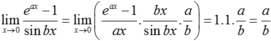
Vậy để 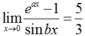 thì
thì 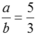 . Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
. Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
+ 15k2 = 15 ⇔ k2 = 1 ⇒ k = 1 ⇒ ab = 15.
+ 15k2 = 60 ⇔ k2 = 4 ⇒ k = 2 ⇒ ab = 60.
+ 15k2 = 240 ⇔ k2 = 16 ⇒ k = 4 ⇒ ab = 240.
Vậy cả ba đáp án đều đúng.
Đúng 0
Bình luận (0)
Cho đa thức f(x)=ax^2+bx+c với a,b,c là các số thực.Biết f(0); f(1); f(2) có giá trị nguyên.CMR: 2a,2b có giá trị nguyên
Chứng minh rằng: \(P\left(x\right)=ax^3+bx^2+cx+d\)có giá trị nguyên với mọi x nguyên khi và chỉ khi 6a, 2b, a+b+c và d là số nguyên.
bài................khó...............quá....................mà...............trời...........lại...............rét................tick..................ủng..............hộ.................mình.................nha.............
Đúng 0
Bình luận (0)
sao bat chuoc tao ha NGuyen ding anh
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Gửi các thành viên BGS
Câu hỏi số 1 - lớp 7
Cho đa thức Px=ax2+bx+c trong đó các hệ số a,b,c là các số nguyên. Biết rằng giá trị của đa thức chia hết cho 3 với mọi giá trị nguyên của x. Chứng minh rằng a, b, c đều chia hết cho 3.
Số các giá trị nguyên x sao cho biểu thức A=\(\frac{3}{x+2}\)nhận giá trị nguyên là
Để \(A=\frac{3}{x+2}\) đạt được giá trị nguyên
=> 3 chia hết x+2
=> \(x+2\inƯ\left(3\right)\)
Mà \(Ư\left(3\right)=\left\{1;-1;3;-3\right\}\)
=> Ta lập được bảng sau:
| x+2 | 1 | -1 | 3 | -3 |
| x | -1 | -3 | 1 | -5 |
Vậy để \(A=\frac{3}{x+2}\) thì x = {-1;-3;1;-5}
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
Hàm số bậc hai
y
f
x
a
2
+
b
x
+
c
a
≠
0
nhận giá trị bằng 1 khi x1 và đạt giá trị nhỏ nhất bằng
3
4
khi
x
1
2
thì có tích các hệ số là A. abc-1 B. abc1 C. abc-3...
Đọc tiếp
Hàm số bậc hai y = f x = a 2 + b x + c a ≠ 0 nhận giá trị bằng 1 khi x=1 và đạt giá trị nhỏ nhất bằng 3 4 khi x = 1 2 thì có tích các hệ số là
A. abc=-1
B. abc=1
C. abc=-3
D. abc=3
CMR: f(x)=ax^3+bx^2+cx+d có giá trị nguyên với mọi x nguyên khi và chỉ khi 6a,2b, a+b+c và d là số nguyên
+) ta có: \(f\left(0\right)=a.0^3+b.0^2+c.0+d=d\)
\(f\left(1\right)=a.1^3+b.1^2+c.1+d=a+b+c+d\)
\(f\left(2\right)=a.2^3+b.2^2+c.2+d=8a+4b+2c+d\)
Nếu f(x) có g/trị nguyên vs mọi x \(\Rightarrow\) d ; a+b+c+d ; 8a+4b+2c+d nguyên
Do d nguyên \(\Rightarrow\) a+b+c nguyên
(a+b+c+d)+(a+b+c+d)+2b nguyên\(\Rightarrow\)2b nguyên\(\Rightarrow\)6b nguyên
+) ta lại có: \(f\left(0\right)=a.0^3+b.0^2+c.0+d=d\)
mà f(0) nguyên nên d nguyên
\(f\left(1\right)=a.1^3+b.1^2+c.1+d=a+b+c+d\)
\(f\left(-1\right)=a.\left(-1\right)^3+b.\left(-1\right)^2+c.\left(-1\right)+d=-a+b-c+d\)
\(\Rightarrow f\left(1\right)+f\left(-1\right)=2b+2d\)
\(\Rightarrow2b=f\left(1\right)+f\left(-1\right)-2d\)\(\Rightarrow\)\(2b\)nguyên
mặt khác: f(2)= 8a+4b+2c+d
\(\Rightarrow\) f(2) - 2f(1) = 6a-2b+d
\(\Rightarrow\) 6a = f(2) - 2f(1)+2b-d
\(\Rightarrow\) 6a nguyên
vậy f(x) = ax^3 + bx^2 + cx + d có giá trị nguyeenvs mọi x nguyên khi và chỉ khi 6a ; 2b ; a+b+c và d là các số nguyên
Bài này có 2 vế nha bn, mk c/m hết r đó, nếu bn thấy dài wa thì thu gọn lại nha! chúc bn hc tốt!
Đúng 0
Bình luận (0)
nhìn thì dài nhưng ko dài lắm đâu, tại mk dùng cỡ chữ to vài chỗ nên nó dài thôi. bài lm ko dài bn cứ lm đi, đừng ngại!
Đúng 0
Bình luận (0)