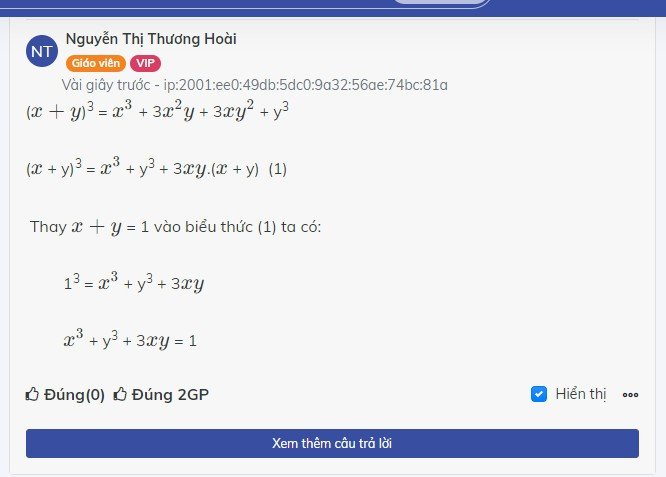
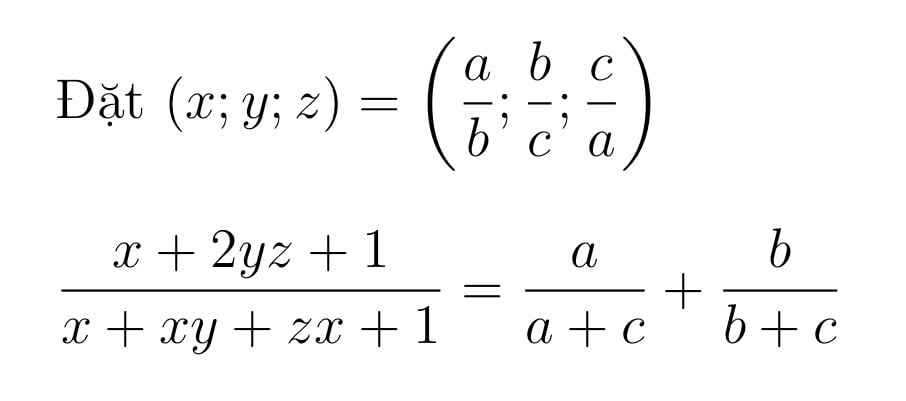cho x+y=1 tính Gia trị biểu thức
M=x^3+3xy+y^3 bằng 2 cách
FL
Những câu hỏi liên quan
cho x+y=1 tính giá trị biểu thức
M=x^3+3xy+y^3 bằng 2 cách
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1
Đúng 0
Bình luận (0)
Cho x+y=1 .tính giá trị biểu thức x3 + y3 +3xy và x-y=1 .Tính giá trị biểu thức x3 - y3-3xy
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
Đúng 0
Bình luận (0)
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
a)Cho x+y=1.Tính giá trị của biểu thức x3+y3+3xy
b)Cho x-y=1.Tính giá trị của biểu thức x3-y3-3xy
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
a) cho x + y = 1 . tính giá trị biểu thức x3 + y3 + 3xy
b) cho x-y= 1. tính giá trị của biểu thức x3 - y3 - 3xy
a) \(x+y=1\)
=> \(\left(x+y\right)^3=1\)
<=> \(x^3+y^3+3xy\left(x+y\right)=1\)
<=> \(x^3+y^3+3xy=1\)
b) \(x-y=1\)
=> \(\left(x-y\right)^3=1\)
<=> \(x^3-y^3-3xy\left(x-y\right)=1\)
<=> \(x^3-y^3-3xy=1\)
Đúng 0
Bình luận (0)
Cho 3 số dương x; y; z thỏa mãn xyz = 1.
Tính giá trị của biểu thức
M = \(\dfrac{x+2xy+1}{x+xy+xz+1}+\dfrac{y+2yz+1}{y+yz+yx+1}+\dfrac{z+2zx+1}{z+zx+z+1}\)
1 . Cho x+ya và x.yb . Tính giá trị biểu thức sau theo a và b :a) x2 + y2b) x3 + y3 c) x4 + y4d) x5 + y52 . Cho x+y1 .Tính giá trị biểu thức x3 + y3 + 3xy và x-y1 .Tính giá trị biểu thức x3 - y3 - 3xy3 . Cho a+b1 . Tính giá trị biểu thức : M a3 + b3 + 3ab .( 12 + b2 ) + 6.a2 .b2 . ( a+b)
Đọc tiếp
1 . Cho x+y=a và x.y=b . Tính giá trị biểu thức sau theo a và b :
a) x2 + y2
b) x3 + y3
c) x4 + y4
d) x5 + y5
2 . Cho x+y=1 .Tính giá trị biểu thức x3 + y3 + 3xy và x-y=1 .Tính giá trị biểu thức x3 - y3 - 3xy
3 . Cho a+b=1 . Tính giá trị biểu thức : M = a3 + b3 + 3ab .( 12 + b2 ) + 6.a2 .b2 . ( a+b)
Cho \(x+y=1\). Tính giá trị biểu thức \(A=x^3+3xy+y^3\)
\(A=x^3+3xy+y^3\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=1.\left(x^2-xy+y^2\right)+3xy\)
\(=x^2-xy+y^2+3xy\)
\(=x^2+2xy+y^2\)
\(=\left(x+y\right)^2\)
\(=1\)
Đúng 0
Bình luận (0)
tính giá trị biểu thức
1)cho x+y=1. tính giá trị biểu thức: x^3+3xy+y^3
2)A= a^3-3a^2+3a+4 với a=11
3)B=1995^3+1/1995^2-1994