nhờ mọi người giúp:
cho a;b;c dương, chứng minh
\(\dfrac{b+c}{a^2+bc}+\dfrac{c+a}{b^2+ca}+\dfrac{a+b}{c^2+ab}\le\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Mọi người ơi em nhờ mọi người xóa nick này giùm với ạ !

bạn nên báo với ad rồi đưa ra lí do vì sao bạn muốn xóa nick bạn ấy á
Trước tui cũng gặp trường hợp như vậy. Bạn đó gửi cả ảnh 18+ vào trong bài trả lời của mình. Sau tui không thấy nick đó hoạt động chắc là kiểm duyệt xóa rồi. Mà không hiểu sao lúc đó mấy anh chị kiểm duyệt lại không chặt chẽ nữa :((
thiệc ra acc đó nhắn cho em mấy ngày rùi ó, em xóa tin nhắn đi lại nhắn tiếp :))
Nhờ mọi người giải giúp cháu phép toán ạ: 84:a=8(d-4)
nhờ mọi người ạ
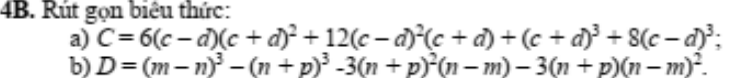
\(C=6\left(c-d\right)\left(c+d\right)\left(c+d\right)+12\left(c-d\right)\left(c-d\right)\left(c+d\right)+c^3+3c^2d+3cd^2+d^3+8\left(c^3-3c^2d+3cd^2-d^3\right)\)
\(C=6\left(c^2-d^2\right)\left(c+d\right)+12\left(c-d\right)\left(c^2-d^2\right)+c^3+3c^2d+3cd^2+d^3+8\left(c^3-3c^2d+3cd^2-d^3\right)\)\(C=6\left(c^3+c^2d-cd^2-d^3\right)+12\left(c^3-c^2d-cd^2-d^2\right)+c^3+3c^2d+3cd^2+d^3+8\left(c^3-3c^2d+3cd^2-d^3\right)\)
\(C=27c^3-27c^2d-39cd^2-25d^3\)
I'd like a ....orange
nhờ mọi người giúp mình với. Thank you
I 'd a juice with orange.
-fun fact
https://www.facebook.com/354675568826928/photos/a.563325071295309/585885745705908/
Em nhờ mọi người vô link trên thả tym giùm em ạ. Đó là cuộc thi do trường em tổ chức ạ. Cảm ơn mọi người nhiều
https://www.facebook.com/354675568826928/photos/a.563325071295309/585885745705908/
nhờ mọi người với ạ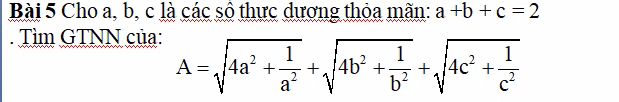
\(A=\sqrt{\left(2a\right)^2+\left(\dfrac{1}{a}\right)^2}+\sqrt{\left(2b\right)^2+\left(\dfrac{1}{b}\right)^2}+\sqrt{\left(2c\right)^2+\left(\dfrac{1}{c}\right)^2}\)
\(A\ge\sqrt{\left(2a+2b+2c\right)^2+\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}\)
\(A\ge\sqrt{4\left(a+b+c\right)^2+\left(\dfrac{9}{a+b+c}\right)^2}=\sqrt{4.2^2+\left(\dfrac{9}{2}\right)^2}=\dfrac{\sqrt{145}}{2}\)
\(A_{min}=\dfrac{\sqrt{145}}{2}\) khi \(a=b=c=\dfrac{2}{3}\)
nhờ mọi người với ạ 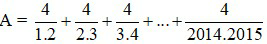
A = 4/(1.2) + 4/(2.3) + 4/(2014.2015)
= 4.[1/(1.2) + 1/(2.3) + ... + 1/(2014.2015)]
= 4.(1 - 1/2 + 1/2 - 1/3 + ... + 1/2014 - 1/2015)
= 4.(1 - 1/2015)
= 4.2014/2015
= 8056/2015
Hello mọi người nhờ sự ủng hộ của mọi người mà hôm nay mình đã làm tốt bài kiểm tra Sử cảm ơn mọi người nhé!
chúc mừng bạn nha lenguyenminhhang
ỦA, tớ ko bít, nhưng tớ Chúc Mừng cậu, được 10 điểm ko?
chứng minh rằng a^7 - a chia hết cho 7.
nhờ mọi người giải thích rõ giúp em ạ.Em cảm ơn
Cách 1: Cái này là định lý Fermat nhỏ thôi bạn. Tổng quát hơn:
Cho số nguyên dương a và số nguyên tố p. Khi đó \(a^p\equiv a\left[p\right]\)
Ta chứng minh định lý này bằng cách quy nạp theo a:
Với \(a=1\) thì \(1^p\equiv1\left[p\right]\), luôn đúng.
Giả sử khẳng định đúng đến \(a=k\left(k\inℕ^∗\right)\). Khi đó \(k^p\equiv k\left[p\right]\). Ta cần chứng minh khẳng định đúng với \(a=k+1\). Thật vậy, với \(a=k+1\), ta có:
\(\left(k+1\right)^p=k^p+C^1_p.k^{p-1}+C^2_pk^{p-2}...+C^{p-1}_pk^1+1\) (*)
((*) áp dụng khai triển nhị thức Newton, bạn có thể tìm hiểu trên mạng)
(Ở đây kí hiệu \(C^n_m=\dfrac{m!}{n!\left(m-n\right)!}\) với \(m\ge n\) là các số tự nhiên và kí hiệu \(x!=1.2.3...x\))
Ta phát biểu không chứng minh một bổ đề quan trọng sau: Với p là số nguyên tố thì \(C^i_p⋮p\) với mọi \(1\le i\le p-1\)
Do đó vế phải của (*) \(\equiv k^p+1\left[p\right]\). Thế nhưng theo giả thiết quy nạp, có \(k^p\equiv k\left[p\right]\) nên \(k^p+1\equiv k+1\left[p\right]\), suy ra \(\left(k+1\right)^p\equiv k+1\left[p\right]\)
Vậy khẳng định đúng với \(a=k+1\). Theo nguyên lí quy nạp, suy ra điều phải chứng minh. Áp dụng định lý này cho số nguyên tố \(p=7\) là xong.
Cách 2: Đối với những số nhỏ như số 7 thì ta có thể làm bằng pp phân tích đa thức thành nhân tử để cm là được:
\(P=a^7-a\)
\(P=a\left(a^6-a\right)\)
\(P=a\left(a^3-1\right)\left(a^3+1\right)\)
\(P=a\left(a-1\right)\left(a+1\right)\left(a^2-a+1\right)\left(a^2+a+1\right)\)
Nếu \(a⋮7,a\equiv\pm1\left[7\right]\) thì hiển nhiên \(P⋮7\)
Nếu \(a\equiv\pm2\left[7\right];a\equiv\pm3\left[7\right]\) thì \(\left(a^2-a+1\right)\left(a^2+a+1\right)⋮7\), suy ra \(P⋮7\). Vậy \(a^7-a⋮7\)