TH
Những câu hỏi liên quan
Tính giá trị của biểu thức 3x2-9x tại x=1 và tại x=1/3
\(3x^2-9x=3x\left(x-3\right)\)
Thế x=1 ta được:
\(3.1\left(1-3\right)=3.-2=-6\)
Thế x=\(\dfrac{1}{3}\) ta được:
\(3.\dfrac{1}{3}\left(\dfrac{1}{3}-3\right)=1-\dfrac{8}{3}=-\dfrac{8}{3}\)
Đúng 1
Bình luận (0)
Thay x=1 vào biểu thức ta có:
\(3x^2-9x=3.1^2-9.1=3-9=-6\)
Thay x=\(\dfrac{1}{3}\) vào biểu thức ta có:
\(3x^2-9x=3x\left(x-3\right)=3.\dfrac{1}{3}\left(\dfrac{1}{3}-3\right)=1.\dfrac{-8}{3}=\dfrac{-8}{3}\)
Đúng 1
Bình luận (0)
câu trả lời là:
ko học toàn đi hỏi bài tự làm thấy tốt hơn hỏi bài phiền thiên hạ hơn anh ơi bỏ đi nhé ko là sau này hỏng đó
anh nhớ tích nhé!
Đúng 0
Bình luận (0)
tính giá trị của các biểu thức sau
A= x^3-3x^2-3x-1 tại x=101
B=x^3+3x^2+3x tại x=99
C=x^3+9x^2+27x tại x=97
D=x^5-15x^4+16x^3-28x^2+13x tại x=14
\(A=x^3-3x^2+3x-1\\ A=x^3-3x^2.1+3x.1^2-1^3\\ A=\left(x-1\right)^3\)
Thay x=101 vào biểu thức trên ta được kết quả là 100^3= 1000000
Đúng 0
Bình luận (0)
Khi x= 101
\(A=x^3-3x^2-3x-1\)
\(\Rightarrow A=101^3-3.101^2-3.101-1\)
\(\Rightarrow A=999394\)
tíc mình nha
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức 3x2 – 9x tại x = 1 và tại x = 1 3 .
- Thay x = 1 vào biểu thức 3x2 – 9x, ta có:
3.12-9.1 = 3.1 - 9 = 3 - 9 = -6
Vậy giá trị của biểu thức 3x2 – 9x tại x = 1 là – 6
- Thay 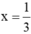 vào biểu thức trên, ta có:
vào biểu thức trên, ta có:
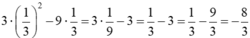
Vậy giá trị của biểu thức 3x2 – 9x tại 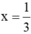 là
là 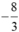
Đúng 0
Bình luận (0)
giúp mik vớinhân các đa thức saua, (1/3x + 2 ) (3x - 6 )b, (x^2 - 3x + 9 ) (x + 3 )c, ( -2xy + 3 ) ( xy +1 )d, x ( xy - 1 ) ( xy + 1 )tính giá trị biểu thứca, M ( 3x + 2 ) ( 9x^2 - 6x + 4 ) tại x 1/3b, N ( 5x - 2y ) ( 25x^2 + 10xy + 4y^2 ) tại x 1/5 và y 1/2chứng minh giá trị của biểu thức sau ko phụ thuộc vào giá trị của biếnA ( x + 2 ) ( 3x - 1 )- x ( 3x + 3 ) - 2x + 7
Đọc tiếp
giúp mik với
nhân các đa thức sau
a, (1/3x + 2 ) (3x - 6 )
b, (x^2 - 3x + 9 ) (x + 3 )
c, ( -2xy + 3 ) ( xy +1 )
d, x ( xy - 1 ) ( xy + 1 )
tính giá trị biểu thức
a, M = ( 3x + 2 ) ( 9x^2 - 6x + 4 ) tại x = 1/3
b, N = ( 5x - 2y ) ( 25x^2 + 10xy + 4y^2 ) tại x= 1/5 và y = 1/2
chứng minh giá trị của biểu thức sau ko phụ thuộc vào giá trị của biến
A= ( x + 2 ) ( 3x - 1 )- x ( 3x + 3 ) - 2x + 7
Bài 1:
a: \(\left(\dfrac{1}{3}x+2\right)\left(3x-6\right)\)
\(=x^2-3x+6x-12\)
\(=x^2+3x-12\)
b: \(\left(x+3\right)\left(x^2-3x+9\right)=x^3+27\)
c: \(\left(-2xy+3\right)\left(xy+1\right)\)
\(=-2x^2y^2-2xy+3xy+3\)
\(=-2x^2y^2+xy+3\)
d: \(x\left(xy-1\right)\left(xy+1\right)\)
\(=x\left(x^2y^2-1\right)\)
\(=x^3y^2-x\)
Đúng 1
Bình luận (0)
Bài 2:
a: Ta có: \(M=\left(3x+2\right)\left(9x^2-6x+4\right)\)
\(=27x^3+8\)
\(=27\cdot\dfrac{1}{27}+8=9\)
b: Ta có: \(N=\left(5x-2y\right)\left(25x^2+10xy+4y^2\right)\)
\(=125x^3-8y^3\)
\(=125\cdot\dfrac{1}{125}-8\cdot\dfrac{1}{8}\)
=0
Đúng 1
Bình luận (0)
Bài 3:
Ta có: \(A=\left(x+2\right)\left(3x-1\right)-x\left(3x+3\right)-2x+7\)
\(=3x^2-x+6x-2-3x^2-9x-2x+7\)
=5
Đúng 1
Bình luận (0)
tính giá trị biểu thức
b x3 - 3x2 + 3x - 1 Tại x =101
c x 3 + 9x2 + 27x tại x = 97
a, \(x^3-3x^2+3x-1=\left(x-1\right)\left(x^2+x+1\right)-3x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2-2x+1\right)=\left(x-1\right)^3\)
Thay x = 101 vào biểu thức trên ta được :
\(\left(101-1\right)^3=100.100.100=1000000\)
b, \(x^3+9x^2+27x\Leftrightarrow x\left(x^2+9x+27\right)\)
Thay x = 97 vào biểu thức trên ta được :
\(97\left[\left(97\right)^2+9.97+27\right]=97.10309=999973\)
bạn xem lại đề ý b nhé
Trả lời:
b, x3 - 3x2 + 3x - 1 = ( x - 1 )3
Thay x = 101 vào biểu thức trên, ta có:
( 101 - 1 )3 = 1003 = 1000000
c, x3 + 9x2 + 27x
Thay x = 97 vào biểu thức trên, ta có:
973 + 9.972 + 27.97 = 999973
b.\(x^3-3x^2+3x-1\)
\(=\left(x-1\right)^3\)
Tại \(x=101\)thì biểu thức có giá trị là
\(\left(x-1\right)^3\)
\(=\left(101-1\right)^3\)
\(=100^3=1000000\)
Xem thêm câu trả lời
câu 5
1, tính giá trị của biểu thức sau:
a, \(x^2+2x+1
tại
x=99\)
b, \(x^3-3x^2+3x-1
tại
x=101\)
2, tìm giá trị lớn nhất của biểu thức
\(A=
-x^2+2xy-4y^2+2x+10y-3\)
1, a)
Ta có:
\(x^2+2x+1=\left(x+1\right)^2\)
Thay x=99 vào ta có:
\(\left(99+1\right)^2=100^2=10000\)
b) Ta có:
\(x^3-3x^2+3x-1=\left(x-1\right)^3\)
Thay x=101 vào ta có:
\(\left(101-1\right)^3=100^3=1000000\)
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức sau :
a, x3-3x2+3x-1 tại x=101
b, x3 +9x2+27x+27 tại x=97
a) \(x^3-3x^2-3x-1\)
\(=\left(x-1\right)^3\)
Với x=101 thì giá trị biểu thức là:
\(\left(101-1\right)^3\)
\(=100^3\)
\(=1000000\)
b) \(x^3+9x^2+27x+27\)
\(=\left(x+3\right)^3\)
Với x=97 thì giá trị biểu thức là:
\(\left(97+3\right)^3\)
\(=100^3\)
\(=1000000\)
Đúng 0
Bình luận (0)
a) \(x^3-3x^2+3x-1\)
\(=\left(x^3-1\right)+\left(-3x^2+3x\right)\)
\(=\left(x-1\right)\left(x^2+x+1\right)-3x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x+1-3x\right)\)
\(=\left(x-1\right)\left(x^2-2x+1\right)\)
\(=\left(x-1\right)\left(x-1\right)^2\)
\(=\left(x-1\right)^3\) \(\left(A\right)\)
thay x=101 vào biều thức A ta được
\(\left(101-1\right)^3\)\(=100^3=1000000\)
vậy giá trị của biểu thức trên là 1000000
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
rút gọn rồi tính giá trị biểu thức
a,\(\dfrac{9x^2-6x+1}{9x^2+1}\) tại x =-3
b, \(\dfrac{x^2-6x+9}{-9x+3x^2}\) tại x=-\(\dfrac{1}{3}\)
c, \(\dfrac{x^2-4x+4}{2x^2-4x}\) tại x=-\(\dfrac{1}{2}\)
a) \(\dfrac{9x^2-6x+1}{9x^2-1}\)
\(=\dfrac{\left(3x-1\right)^2}{\left(3x-1\right)\left(3x+1\right)}\)
\(=\dfrac{3x-1}{3x+1}\)
\(=\dfrac{3\cdot\left(-3\right)-1}{3\cdot\left(-3\right)+1}=\dfrac{-9-1}{-9+1}=\dfrac{-10}{-8}=\dfrac{5}{4}\)
b) Ta có: \(\dfrac{x^2-6x+9}{3x^2-9x}\)
\(=\dfrac{\left(x-3\right)^2}{3x\left(x-3\right)}\)
\(=\dfrac{x-3}{3x}\)
\(=\dfrac{-\dfrac{1}{3}-3}{3\cdot\dfrac{-1}{3}}=\dfrac{-\dfrac{10}{3}}{-1}=\dfrac{10}{3}\)
c) Ta có: \(\dfrac{x^2-4x+4}{2x^2-4x}\)
\(=\dfrac{\left(x-2\right)^2}{2x\left(x-2\right)}\)
\(=\dfrac{x-2}{2x}\)
\(=\dfrac{\dfrac{-1}{2}-2}{2\cdot\dfrac{-1}{2}}=\dfrac{-\dfrac{5}{2}}{-1}=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Tính giá trị biểu thức
a) x^2y^2 tại x=87,y-13
b) x^3-3x^2+3x-1 tại x- 101
c) x^3+9x^2+27x+27 tại x= 97
tính nhanh hợp lí, áp dụng các hằng thức đáng nhớ, giải chi tiết
a) x2-y2
= (x-y)x(x+y)
=(87+13)x(87-13)
=100x74
=7400
b) x3-3x2+3x-1
=x3-3x21+3x12-13=(x-1)3
=(101-1)3
=1003
=1000000
c) x3+9x2+27x+27
=x3+3x23+3x32+33
=(x+3)3
=(97+3)3
=1003
=1000000
Bài cũn dễ mà ![]()
Đúng 0
Bình luận (0)





