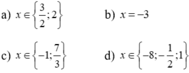-12x(x - 5) + 7x(3 - x) = 5

-12x² + 60 + 21x - 7x² = 5

-19x² + 21x + 60 - 5 = 0

-19x² + 21x + 55 = 0 

\(\Delta=b^2-4ac=21^2-4.55.\left(-19\right)=441+4180=4621>0\)

vậy phtrinh có hai nghiệm phân biệt:

\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-21+\sqrt{4621}}{2.\left(-19\right)}=\frac{-21+\sqrt{4621}}{-38}\)

\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-21-\sqrt{4621}}{2.\left(-19\right)}=\frac{-21-\sqrt{4621}}{-38}\)

\(-12x\left(x-5\right)+7x\left(3-x\right)=5\)

\(-12x^2+60+21x-7x^2=5\)

\(-19x^2+60+21x=5\)

\(-19x^2+21x=5-60=-55\)

\(-19x^2+21x+55=0\)

\(a=-19;b=-21;c=55\)

\(=B^2-4ac\)

\(=21^2-4\left(-19\right).55\)

\(\Delta=4621\)

Giá trị delta cao hơn 0, vì vậy pt có hai nghiệm 

\(x_1=\frac{-b-\sqrt{\Delta}}{2a};x_2=\frac{-b+\sqrt{\Delta}}{2a}\)

\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{\left(-21\right)-\sqrt{4621}}{2.\left(-19\right)}=\frac{-21-\sqrt{4621}}{-38}\)

\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-21+\sqrt{4621}}{2.\left(-19\right)}=\frac{-21+\sqrt{4621}}{-38}\)

\(-12x\left(x-5\right)+7x\left(3-x\right)=5\)

\(\Leftrightarrow-12x^2+60+21x-7x^2=5\)

\(\Leftrightarrow-19x^2+21x+55=0\)

Ta có \(\Delta=21^2+4.55.19=4621\)

\(\Rightarrow\orbr{\begin{cases}x=\frac{-21+\sqrt{4621}}{-38}\\x=\frac{-21-\sqrt{4621}}{-38}\end{cases}}\)

a) \(^{x^3}\) - 7x+6=0

\(\Leftrightarrow\) \(^{x^3}\) - x-6x+6=0

\(\Leftrightarrow\) \(\left(x^3-x\right)\) - \(\left(6x-6\right)\) =0

\(\Leftrightarrow\) x\(\left(x^2-1\right)\) - 6\(\left(x-1\right)\) =0

\(\Leftrightarrow\) x\(\left(x+1\right)\)\(\left(x-1\right)\) - 6\(\left(x-1\right)\) =0

\(\Leftrightarrow\) \(\left(x-1\right)\) \(\left[x-6\left(x+1\right)\right]\) =0

\(\Leftrightarrow\) \(\left(x-1\right)\) \(\left(6-5x\right)\) =0

\(\Leftrightarrow\) \(\left[\begin{matrix}x-1=0\\6-5x=0\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left[\begin{matrix}x=1\\5x=-6\end{matrix}\right.\)

\(\Leftrightarrow\) \(\left[\begin{matrix}x=1\\x=-\frac{6}{5}\end{matrix}\right.\)

Những câu sau dùng phương pháp phân tích đa thức thành nhân tử nhé!

x⁴- 4x³+3x²+4x-4= 0

(x-1)(x+1)(x-2)²=0

x=1 ;x=-1;x=2

a)x^3 - 7x - 6

= x^3 + x^2 - x^2 - 6x - x - 6

= (x^3 + x^2) - (x^2 + x) - (6x + 6)
= x^2(x + 1) - x(x + 1) - 6(x + 1)

= (x + 1)(x^2 - x - 6)

= (x + 1)(x^2 - 3x + 2x - 6)
= (x + 1){(x^2 - 3x) + (2x - 6)}

= (x + 1){(x(x - 3) + 2(x - 3)}
= (x + 1)(x - 3)(x + 2)

\(-12.\left(x-5\right)+7.\left(3-x\right)=5\)

\(\Rightarrow-12x+60+21-7x=5\)

\(\Rightarrow-12x-7x=5-60-21\)

\(\Rightarrow-19x=-76\)

\(\Rightarrow x=4\)

Vậy x = 4

-12x(X-5)+7x(3-X)=5-12x(X-5)+7x(3-X)=5-12x(X-5)+7x(3-X)=5

b. sửa đề

\(6x^4+25x^3+12x-25x^2+6=0\)

\(\Leftrightarrow6x^4+12x^3+13x^3+26x^2-14x^2-28x+3x+6=0\)

\(\Leftrightarrow6x^3\left(x+2\right)+13x^2\left(x+2\right)-14x\left(x+2\right)+3\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(6x^3+13x^2-14x+3\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x+3\right)\left(2x-1\right)\left(3x-1\right)=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=-3\\x=\dfrac{1}{2}\\x=\dfrac{1}{3}\end{matrix}\right.\)

Vậy........

Bài 1 : Giải phương trình

a) (x + 3)⁴ + (x + 5)⁴ = 16

Đặt : x + 3 = t

=> x + 5 = x + 3 + 2 = t + 2

Thay x + 3 = t và x + 5 = t + 2 vào phương trình, ta có :

t⁴ + (t + 2)⁴ = 16

<=> 2t⁴ + 8t³ + 24t² + 32t + 16 = 16

<=> 2(t⁴ + 4t³ + 12t² + 16t) = 0

<=> t⁴ + 4t³ + 12t² + 16t = 0

<=> (t + 2) . t . (t² + 2y + 4) = 0

TH1 : t = 0

TH2 : t + 2 = 0 <=> t = -2

TH3 : t² + 2y + 4 = 0 (vô nghiệm => loại)

Nên t = 0 hoặc t = -2

hay x + 3 = -2 hoặc x + 3 = 0

<=> x = -5 hoặc x = -3

\(S=\left\{-5;-3\right\}\)

b) 6x⁴ + 25x³ + 12x² - 25x + 6 = 0

<=> 6x⁴ + 12x³ + 13x³ + 26x² - 14x² - 28x + 3x + 6 = 0

<=> 6x³ (x + 2) + 13x² (x + 2) - 14x (x + 2) + 3(x + 2) = 0

<=> (x + 2)(6x³ + 13x² - 14x + 3) = 0

<=> (x + 2)(6x³ + 18x² - 5x² - 15x + x + 3) = 0

\(\Leftrightarrow\left(x+2\right)[6x^2\left(x+3\right)-5x\left(x+3\right)+\left(x+3\right)]=0\)

<=> (x + 2)(x + 3) (6x² - 5x + 1) = 0

<=> (x + 2)(x + 3)(2x - 1)(3x - 1) = 0

TH1 : x + 2 = 0 <=> x = -2

TH2 : x + 3 = 0 <=> x = -3

TH3 : 2x - 1 = 0 <=> 2x = 1 <=> x = \(\dfrac{1}{2}\)

TH4 : 3x - 1 = 0 <=> 3x = 1 <=> 3x = \(\dfrac{1}{3}\)

\(S=\left\{-2;-3;\dfrac{1}{2};\dfrac{1}{3}\right\}\)

\(\text{a) }\left(x+3\right)^4+\left(x+5\right)^4=16\\ \Leftrightarrow\left(x^2+6x+9\right)^2+\left(x^2+10x+25\right)^2=16\\ \Leftrightarrow x^4+36x^2+81+12x^3+18x^2+108x+x^4+100x^2+625+20x^3+50x^2+500x=16\\ \Leftrightarrow2x^4+32x^3+204x^2+608x+690=0\\ \Leftrightarrow x^4+16x^3+102x^2+304x+345=0\\ \Leftrightarrow x^4+5x^3+11x^3+55x^2+47x^2+235x+373x+69x+345=0\\ \Leftrightarrow\left(x^4+5x^3\right)+\left(11x^3+55x^2\right)+\left(47x^2+235x\right)+\left(69x+345\right)=0\\ \Leftrightarrow x^3\left(x+5\right)+11x^2\left(x+5\right)+47x\left(x+5\right)+69\left(x+5\right)=0\\ \Leftrightarrow\left(x^3+11x^2+47x+69\right)\left(x+5\right)=0\\ \Leftrightarrow\left(x^3+3x^2+8x^2+24x+23x+69\right)\left(x+5\right)=0\\ \Leftrightarrow\left[\left(x^3+3x^2\right)+\left(8x^2+24x\right)+\left(23x+69\right)\right]\left(x+5\right)=0\\ \Leftrightarrow\left[x^2\left(x+3\right)+8x\left(x+3\right)+23\left(x+3\right)\right]\left(x+5\right)=0\\ \Leftrightarrow\left(x^2+8x+23\right)\left(x+3\right)\left(x+5\right)=0\)\(\Leftrightarrow\left(x^2+8x+16+7\right)\left(x+3\right)\left(x+5\right)=0\\ \Leftrightarrow\left[\left(x+4\right)^2+7\right]\left(x+3\right)\left(x+5\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x+5\right)=0\left(\text{Vì }\left(x+4\right)^2+7\ne0\right)\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-5\end{matrix}\right.\)

Vậy tập nghiệm phương trình là \(S=\left\{-3;-5\right\}\)

gần giống avatar của mk