 Giúp em câu b , c
Giúp em câu b , c
Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng
Giúp em câu b và câu c với ạ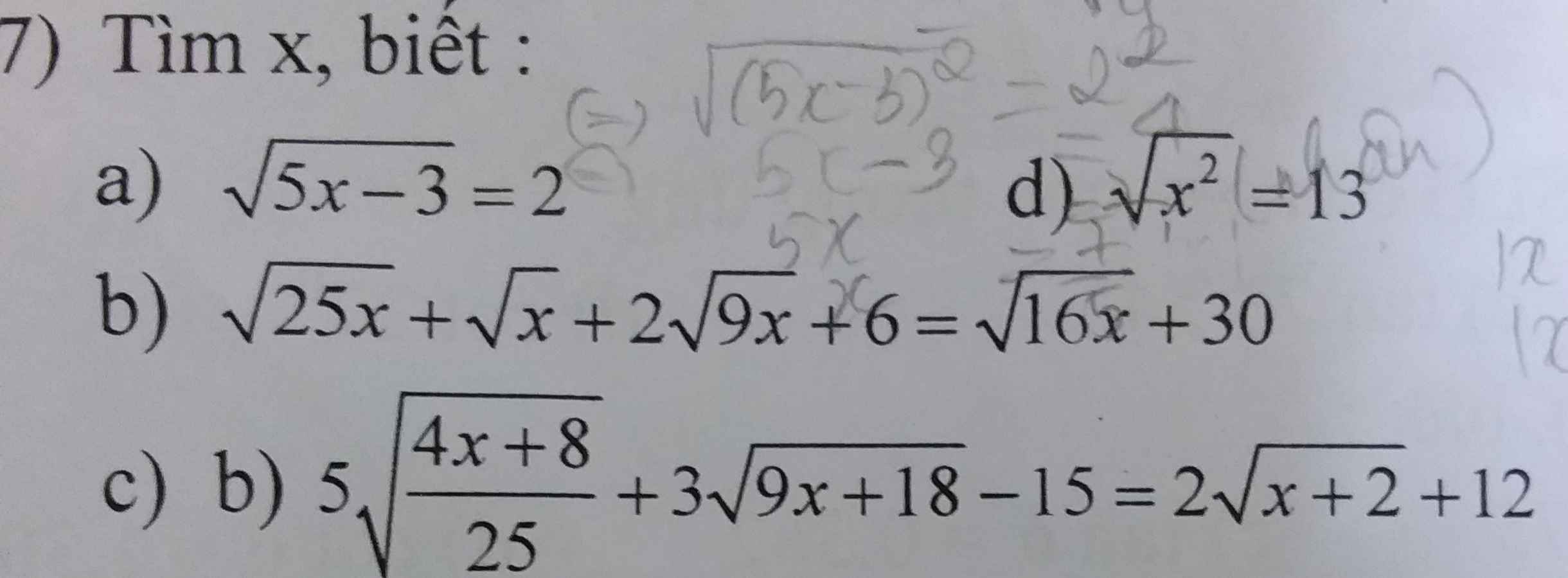
\(a,\Leftrightarrow5x-3=4\Leftrightarrow x=\dfrac{12}{5}\\ b,ĐK:x\ge0\\ PT\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}+6=4\sqrt{x}+30\\ \Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ c,ĐK:x\ge-2\\ PT\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-15=2\sqrt{x+2}+12\\ \Leftrightarrow9\sqrt{x+2}=27\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\\ \Leftrightarrow x=7\left(tm\right)\\ d,\Leftrightarrow\left|x\right|=13\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-13\end{matrix}\right.\)
a: \(\Leftrightarrow5x-3=4\)
hay \(x=\dfrac{7}{5}\)
b) ĐKXĐ: \(x\ge0\)
\(pt\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}-4\sqrt{x}=30-6\)
\(\Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\)
c) ĐKXĐ: \(x\ge-2\)
\(pt\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-2\sqrt{x+2}=12+15\)
\(\Leftrightarrow9\sqrt{x+2}=27\Leftrightarrow\sqrt{x+2}=3\)
\(\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\)
Giúp em với và cảm ơn ạ. Em cần giúp câu b, c, d ạ
a: \(\widehat{C}=30^0\)
Giúp em câu b và câu d ạ!
Em cũng cảm ơn anh NGUYỄN LÊ PHƯỚC THỊNH đã trả lời câu a và câu c
b) Ta có: \(\left(-\dfrac{1}{2}\right)^2\cdot2\dfrac{6}{7}-\dfrac{14}{15}:2\dfrac{1}{3}+\left(-1.21\right)^0\)
\(=\dfrac{1}{4}\cdot\dfrac{20}{7}-\dfrac{14}{15}:\dfrac{7}{3}+1\)
\(=\dfrac{5}{7}-\dfrac{14}{15}\cdot\dfrac{3}{7}+1\)
\(=\dfrac{5}{7}-\dfrac{2}{5}+1\)
\(=\dfrac{25-14-35}{35}=\dfrac{-24}{35}\)
Giúp em câu b và c với ạ, em cần gấp

b: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB
Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)
hay \(AB^2=BH\cdot BC\)
Giúp em câu a, b, c câu 2 với ạ (•ө•)♡
b: \(\Leftrightarrow x\sqrt{2}=2\sqrt{2}+5\sqrt{2}=7\sqrt{2}\)
hay x=7
GIÚP EM CÂU C,D BÀI 1,CÂU B,D BÀI 2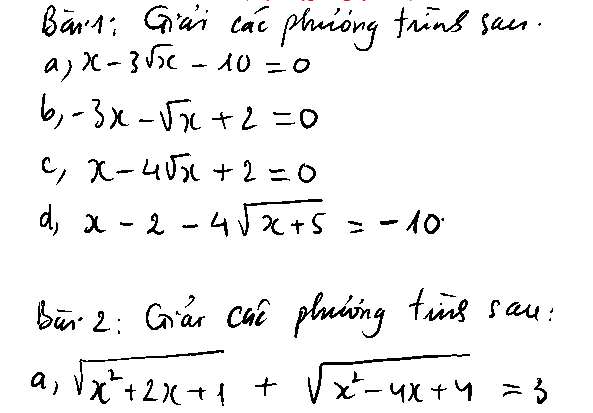
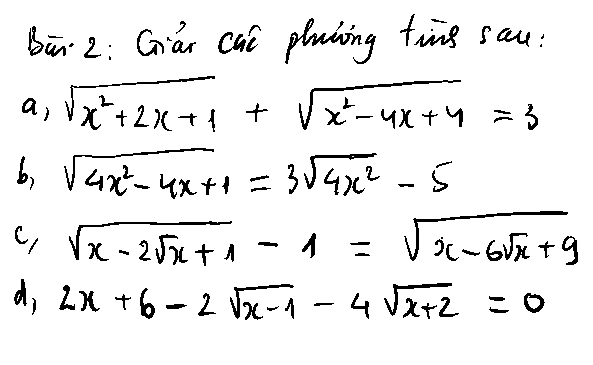
1.
d, ĐK: \(x\ge-5\)
\(x-2-4\sqrt{x+5}=-10\)
\(\Leftrightarrow x+5-4\sqrt{x+5}+3=0\)
\(\Leftrightarrow\left(\sqrt{x+5}-1\right)\left(\sqrt{x+5}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=1\\\sqrt{x+5}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=1\\x+5=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=4\end{matrix}\right.\)
\(\Leftrightarrow x=\pm4\left(tm\right)\)
2.
ĐK: \(x\in R\)
\(\sqrt{x^2+2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left|x+1\right|+\left|x-2\right|=3\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\).
\(\left|x+1\right|+\left|x-2\right|=\left|x+1\right|+\left|2-x\right|\ge\left|x+1+2-x\right|=3\)
Đẳng thức xảy ra khi:
\(\left(x+1\right)\left(2-x\right)\ge0\)
\(\Leftrightarrow-1\le x\le2\)
a)\(\left(\left(\sqrt{x}\right)^2-2\sqrt{x}\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{49}{4}=0\)
⇒\(\left(\sqrt{x}-\dfrac{3}{2}\right)^2=\dfrac{49}{4}\)
TH1:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{7}{2}\)⇒\(\sqrt{x}=5\)⇒x=25
TH2:\(\sqrt{x}-\dfrac{3}{2}=\dfrac{-7}{2}\)⇒\(\sqrt{x}=-2\) vì \(\sqrt{x}\)≥0 loại
GIÚP EM CÂU B,C ẠAA
1: Thay x=16 vào A, ta được:
\(A=\dfrac{4-1}{4+3}=\dfrac{3}{7}\)
2: \(P=A:B\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}:\dfrac{x-3\sqrt{x}-x-6\sqrt{x}-9+x+11\sqrt{x}+6}{x-9}\)
\(=\dfrac{\sqrt{x}-1}{1}\cdot\dfrac{\sqrt{x}-3}{x+2\sqrt{x}-3}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)