Giúp mk vs mng ơi, 5ph mk ph nộp r!!! ![]()

VM
Những câu hỏi liên quan
MN ơi giúp mk vs ạ , mk sắp phải nộp r 😥
Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)(1)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\)(2)
Ta có: M là trung điểm của BC(gt)
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC(đpcm)
Đúng 0
Bình luận (0)
Giúp mk vs mng ơi mk đang cần gấp:'>
a: Xét tứ giác AICK có
AI//CK
AK//CI
Do đó: AICK là hình bình hành
Đúng 0
Bình luận (0)
giúp mk vs mng ơi T_T
a: Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
góc B chung
=>ΔBDA đồng dạng với ΔBFC
=>BD/BF=BA/BC
=>BD*BC=BF*BA và BD/BA=BF/BC
b: Xét ΔBDF và ΔBAC có
BD/BA=BF/BC
góc DBF chung
=>ΔBDF đồng dạng với ΔBAC
c: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
=>ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>BD*BC=BH*BE
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CF*CH=CD*CB
=>BH*BE+CH*CF=BC^2
Đúng 1
Bình luận (0)
Ví dụ về hàm ý trong đời sống hằng ngày
MNG GIÚP MK VS Ạ MAI MK P NỘP
MK CẢM ƠN
mng ơi giúp mình vs ạ .mình cần gấp .mk camon ạ

1............to work by car everyday
2 ........Khanh does morning exercise, he won't keep fit
3......has a small garden
4 .....has to go to school on time
5 ......she doesn't go to bed early, she will be late for class
6 .......go to the movie tonight
\(\text{⩷!⨙┏⇴⨗⨜}\)
Đúng 3
Bình luận (0)
Giúp mk vs mai mk phải nộp r
a: Xét ΔDBH có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔDBH cân tại B
b: AC=10cm
=>AB=5cm
\(BC=\sqrt{5^2+10^2}=5\sqrt{5}\left(cm\right)\)
Đúng 0
Bình luận (0)
Giúp mk vs mai mk phải nộp r
-Hình vẽ:
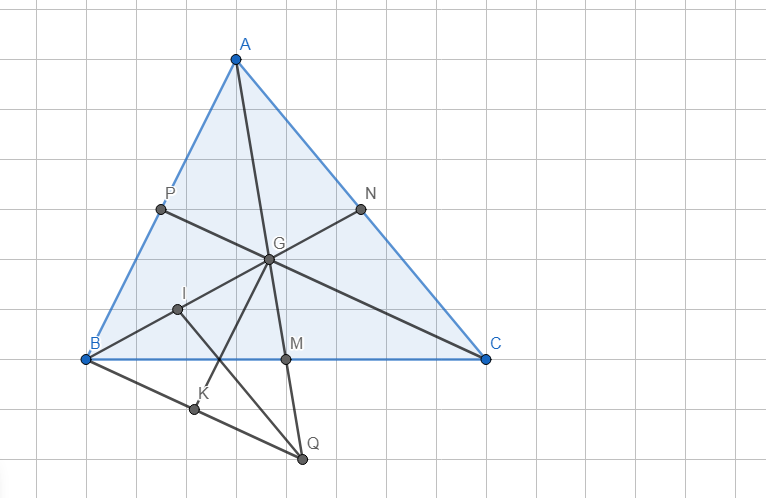
a) -Xét △ABC có:
AM là trung tuyến (gt).
BN là trung tuyến (gt).
G là giao của AM và BN (gt)
=>G là trọng tâm của △ABC.
=>\(BG=\dfrac{2}{3}BN\)(1) (t/c trọng tâm).
\(CG=\dfrac{2}{3}CP\) (2) (t/c trọng tâm).
\(AG=\dfrac{2}{3}AM=2GM\) (t/c trọng tâm).
Mà \(GQ=2GM\) (M là trung điểm GQ).
=>\(GQ=AG=\dfrac{2}{3}AM\) (3).
-Từ (1),(2),(3) suy ra: Độ dài các đường trung tuyến của △BGQ bằng \(\dfrac{1}{2}\) độ dài các cạnh tương ứng của △ABC.
b) -Xét △BMQ và △CMG ta có:
\(BM=CM\) (M là trung điểm của BC).
\(\widehat{BMQ}=\widehat{CMG}\) (đối đỉnh).
\(MQ=MG\) (M là trung điểm GQ)
=>△BMQ = △CMG (c-g-c).
=>\(BQ=CG\) (2 cạnh tương ứng).
-Ta có: \(BC< BG+CG\) (bất đẳng thức trong △BGC).
=>\(BC< BG+BQ\) (\(BQ=CG\))
=>\(\dfrac{1}{2}BC< \dfrac{1}{2}\left(BG+BQ\right)\)
Mà \(BM=\dfrac{1}{2}BC\) (M là trung điểm BC).
=>\(BM< \dfrac{1}{2}\left(BG+BQ\right)\).
c) -Ta có: \(BG=2GN\) (G là trọng tâm của △ABC).
Mà \(BG=2IG\) (I là trung điểm của BG).
=>\(GN=IG\).
-Xét △IQG và △NAG có:
\(IG=NG\) (cmt).
\(\widehat{IGQ}=\widehat{NQA}\) (đối đỉnh).
\(QG=AG\) (cmt).
=>△IQG = △NAG (c-g-c).
=>\(IQ=AN\) (2 cạnh tương ứng) mà \(AN=\dfrac{1}{2}AC\) (N là trung điểm AC).
=>\(IQ=\dfrac{1}{2}AC\) (4).
-Ta có: \(CG=2GP\) (G là trọng tâm của △ABC).
Mà \(BQ=2BK\) (K là trung điểm BQ) và \(BQ=CG\) (cmt).
=>\(GP=BK\).
-Ta có: \(\widehat{BQM}=\widehat{CGM}\)(△BMQ = △CMG).
Mà 2 góc này ở vị trí so le trong.
=>BQ//CG.
-Xét △GBK và △BGP có:
\(BK=GP\left(cmt\right)\)
\(\widehat{KBG}=\widehat{PGB}\) (BK//PQ và so le trong).
\(BG\) là cạnh chung.
=>△GBK = △BGP (c-g-c).
=>\(GK=BP\) (2 cạnh tương ứng) mà \(BP=\dfrac{1}{2}AB\) (P là trung điểm AB).
=>\(GK=\dfrac{1}{2}AB\) (2).
-Từ (1) và (2) và \(BM=\dfrac{1}{2}BC\) (M là trung điểm BC) suy ra:
Độ dài các đường trung tuyến của △BGP bằng \(\dfrac{1}{2}\) độ dài các cạnh tương ứng của △ABC.
Đúng 0
Bình luận (0)
Ae giúp mình với:1+4+9+16+.............+2500.Mk bt kết quả r nhưng chưa bt cách làm mng giúp mk vs

MN ƠI GIÚP MK VS MK CẦN BÀI 1 GẤP LẮM R LM ƠN GIÚP MK VS MK CẢM ƠN





