Mọi người ơi, có thể giúp em bài này được không ạ, em cảm ơn ạ
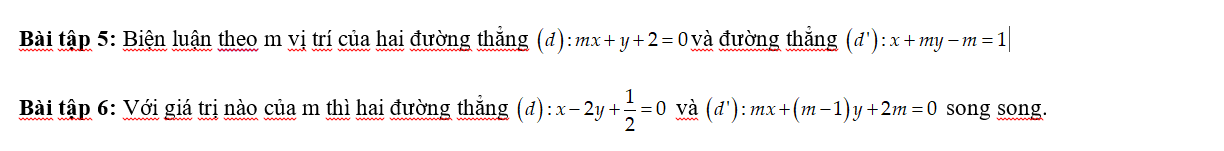
Mọi người ơi, có thể giúp em bài này và vẽ hình giúp em được không ạ, em cảm ơn rất nhiều ạ.
a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp
mọi người ơi, mọi người có thể giúp em làm vài bài này được không ạ tại vì em không làm được với cả ngày mai em phải nộp rồi em cảm ơn ạ!!






Mọi người ơi, có thể giúp em giải bài này được không ạ. Em cần gấp lắm ạ.Em cảm ơn rất nhiều ạ.
a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2
Mọi người ơi, có thể giúp em bài này với không ạ, em cảm ơn rất nhiều ạ.
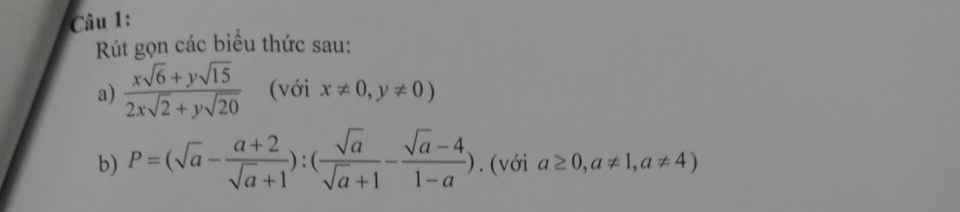
a: \(=\dfrac{\sqrt{3}\left(x\sqrt{2}+y\sqrt{5}\right)}{2\left(x\sqrt{2}+y\sqrt{5}\right)}=\dfrac{\sqrt{3}}{2}\)
b: \(=\dfrac{a+\sqrt{a}-a-2}{\sqrt{a}+1}:\dfrac{a-\sqrt{a}+\sqrt{a}-4}{a-1}\)
\(=\dfrac{\left(\sqrt{a}-2\right)}{\sqrt{a}+1}\cdot\dfrac{a-1}{a-4}=\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\)
mọi người giúp em bài này được không ạ ....
người giúp em bài này được không ạ ....
em cảm ơn mọi người nhiều ạ
post vừa rồi bị lỗi ảnh nên em post lại ạ ...
a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Mọi người ơi, giúp em mấy bài này với ạ. Hàng tá bài mà cô yêu cầu ngày mai nộp gấp quá, em không biết làm sao giờ. Cảm ơn mọi người ạ. 
8: Ta có: \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
\(=\sqrt{5}+1-\sqrt{5}+1\)
=2
Mọi người ơi, giúp em bài này với ạ, em cảm ơn rất nhiều ạ.
Gọi vận tốc của ô tô là x
=>Vận tốc xe máy là x-10
Theo đề, ta có: 120/(x-10)-120/x=1
=>(120x-120x+1200)/x(x-10)=1
=>x^2-10x=1200
=>x^2-10x-1200=0
=>x=40

Có thể giúp em bài 14 được không ạ? Chỉ bài 14 thôi ạ! Cảm ơn mọi người
Bài 14:
a)
Sửa đề: \(AE\cdot AB=AD\cdot AC\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AE\cdot AB=AD\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(cmt)
nên \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADB vuông tại D có
\(\cos\widehat{A}=\dfrac{AD}{AB}\)
Xét ΔAED và ΔACB có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔAED∼ΔACB(c-g-c)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{ED}{CB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}\cdot BC=DE\)
\(\Leftrightarrow DE=BC\cdot\cos\widehat{A}\)(đpcm)
c) Ta có: \(DE=BC\cdot\cos\widehat{A}\)(cmt)
nên \(DE=BC\cdot\cos60^0=\dfrac{1}{2}BC\)(1)
Ta có: ΔEBC vuông tại E(gt)
mà EM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(EM=\dfrac{1}{2}BC\)(2)
Ta có: ΔDBC vuông tại D(gt)
mà DM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(DM=\dfrac{1}{2}BC\)(3)
Từ (1), (2) và (3) suy ra ME=MD=DE
hay ΔMDE đều(đpcm)
Mọi người giúp em làm mấy bài này được không ạ,em sắp thi tới nơi rồi ạ,mọi người làm giúp em thì em cảm ơn ạ 😘😘😘😘