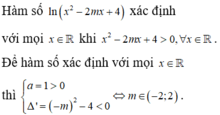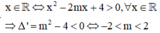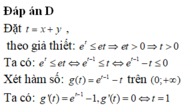PH
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để hàm số
f
(
x
)
sin
x
-
m
sin
2
x
-
1
3
sin
3
x
+
2
m
x
có
f
(
x
)
≥
0
với mọi
x
∈
ℝ
. A.
m
∈
[
1
;
+
∞
)
B.
m
∈...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số f ( x ) = sin x - m sin 2 x - 1 3 sin 3 x + 2 m x có f ' ( x ) ≥ 0 với mọi x ∈ ℝ .
A. m ∈ [ 1 ; + ∞ )
B. m ∈ - 1 ; 1
C. m ∈ ( - ∞ ; - 1 ]
D. m ∈ 1 ; 2
Đáp án A.
Ta có f ' ( x ) = = cos x - 2 m cos 2 x - cos 3 x + 2 m = cos x - cos 3 x - 2 m ( cos 2 x - 1 )
Hàm số có f ' ( x ) ≥ 0 , ∀ x ∈ ℝ ⇔ cos x - cos 3 x ≥ 2 m cos 2 x - 1 , ∀ x ∈ ℝ . (*)
Với cos 2 x = 1 thì thỏa mãn (*).
Với cos 2 x ≢ 1 thì ⇔ cos x - cos 3 x cos 2 x - 1 ≤ 2 m , ∀ x ∈ ℝ .
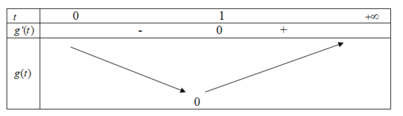
Đặt cos x - cos 3 x cos 2 x - 1 = g ( x ) . Để g ( x ) ≤ 2 m , ∀ x ∈ ℝ , thì 2 m ≥ m a x R g ( x ) .
Sử dụng máy tính cầm tay ta có
![]()
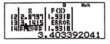
Từ bảng giá trị kết hợp với phương án thì ta suy ra
m a x ℝ g ( x ) = 2 ⇔ 2 m ≥ 2 ⇔ m ≥ 1 .
Đúng 0
Bình luận (0)
cho biểu thức f(x,y)= \(x^2+2y^2-2xy+2mx+2y+25\) ( m là tham số). Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để f(x,y) \(\ge\) 0 với x, y thuộc R. tính tổng tất cả các phần tử của S
\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)
Đúng 1
Bình luận (2)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
ln
x
2
-
2
m
x
+
4
xác định với mọi
x
∈
ℝ
. A.
m
∈
-
∞
;
-
2
∪...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ln x 2 - 2 m x + 4 xác định với mọi x ∈ ℝ .
A. m ∈ - ∞ ; - 2 ∪ 2 ; + ∞
B. m ∈ - 2 ; 2
C. m ∈ - ∞ ; - 2 ∪ 2 ; + ∞
D. m ∈ - 2 ; 2
Đáp án D.
Hàm số xác định với mọi x ∈ ℝ ⇔ x 2 - 2 m x + 4 > 0 , ∀ x ∈ ℝ ⇒ ∆ ' = m 2 - 4 < 0 ⇔ - 2 < m < 2 .
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
ln
x
2
−
2
m
x
+
4
xác định với mọi
x
∈
ℝ
. A.
m
∈
−
2
;
2
B....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ln x 2 − 2 m x + 4 xác định với mọi x ∈ ℝ .
A. m ∈ − 2 ; 2
B. m ∈ − 2 ; 2
C. m ∈ − ∞ ; − 2 ∪ 2 ; + ∞
D. m ∈ − ∞ ; − 2 ∪ 2 ; + ∞
Tìm tất cả các giá trị thực của tham số m để hàm số
y
ln
x
2
-
2
m
x
+
4
xác định với mọi
x
∈
ℝ
. A.
m
∈
-
2
;
2
B.
m
∈
-
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ln x 2 - 2 m x + 4 xác định với mọi x ∈ ℝ .
A. m ∈ - 2 ; 2
B. m ∈ - 2 ; 2
C. m ∈ - ∞ ; - 2 ∪ 2 ; + ∞
D. m ∈ - ∞ ; - 2 ∪ 2 ; + ∞
Tìm tất cả các giá trị thực của tham số m để hàm số
y
ln
x
2
−
2
m
x
+
4
xác định với mọi
x
∈
ℝ
.
A.
m
∈
−
∞
;
−
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = ln x 2 − 2 m x + 4 xác định với mọi x ∈ ℝ .
A. m ∈ − ∞ ; − 2 ∪ 2 ; + ∞
B. m ∈ − 2 ; 2
C. m ∈ − 2 ; 2 ∪ 2 ; + ∞
D. m ∈ − 2 ; 2
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
-
x
3
-
6
x
2
+
(
4
m
-
9
)
x
+
4
nghịch biến trên khoảng
-
∞
;
-
1
là A.
(
-
∞
;...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = - x 3 - 6 x 2 + ( 4 m - 9 ) x + 4 nghịch biến trên khoảng - ∞ ; - 1 là
A. ( - ∞ ; 0 ]
B. [ - 3 4 ; + ∞ )
C. ( - ∞ ; - 3 4 ]
D. [ 0 ; + ∞ )