cho x,y,z khác 0 và x-y-z=0.Tính giá trị biểu thức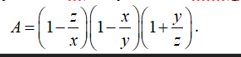
đề cương này khó quá cíu zới:<
QN
Những câu hỏi liên quan
Cho x, y, z đôi một khác nhau và \(\dfrac{1}{x}\)+\(\dfrac{1}{y}\)+\(\dfrac{1}{z}\) = 0
Tính giá trị của biểu thức: M = \(\dfrac{yz}{x^2+2yz}+\dfrac{xz}{y^2+2xz}+\dfrac{xy}{z^2+2xy}\)
Giúp mk giải bài này với, khó quá :((
Bài này ez thôi, làm mãi rồi.
Theo đề bài, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
=>\(\dfrac{xy+yz+xz}{xyz}=0\)
=> xy+yz+zx=0
=> \(\left\{{}\begin{matrix}xy=-yz-zx\\yz=-xy-zx\\zx=-xy-yz\end{matrix}\right.\)
Ta có: x2+2yz=x2+yz-xy-zx=(x-y)(x-z)
y2+2xz=y2+xz-xy-yz=(x-y)(z-y)
z2+2xy=z2+xy-yz-xz=(x-z)(y-z)
=> \(\dfrac{yz}{\left(x-y\right)\left(x-z\right)}+\dfrac{xz}{\left(x-y\right)\left(z-y\right)}+\dfrac{xy}{\left(x-z\right)\left(y-z\right)}=\dfrac{yz\left(y-z\right)-xz\left(x-z\right)+xy\left(x-y\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}=\dfrac{\left(x-y\right)\left(x-z\right)\left(y-z\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}=1\)
Đúng 2
Bình luận (2)
Cho x,y,z khác 0 và x-y-z=0
Tính giá trị của biểu thức: B=(1-z/x)(1-x/y)(1+y/z)
giúp mk zới
Ta có: x-y-z = 0
\(\Rightarrow\) x = y+z
\(\Rightarrow\)y = x-z
\(\Rightarrow\)z = x-y
Thay vào B ta suy ra: \(\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)
= \(\left(1-\frac{x-y}{x}\right)\left(1-\frac{y+z}{y}\right)\left(1+\frac{x-z}{z}\right)\)
= \(\left(\frac{-y}{x}\right).\left(\frac{z}{y}\right).\left(\frac{x}{z}\right)\)
= -y/y
= -1
Vậy B = -1
Đúng 0
Bình luận (0)
cho x,y,z khác nhau và khác 0 và 1/x+1/y+1/z=0
tính giá trị biểu thức : A= y+z/x+z+x/y+x+y/z
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\Rightarrow\frac{1}{x}+\frac{1}{y}=-\frac{1}{z};\frac{1}{x}+\frac{1}{z}=-\frac{1}{y};\frac{1}{y}+\frac{1}{z}=-\frac{1}{x}\)
\(A=\frac{y+z}{x}+\frac{x+z}{y}+\frac{x+y}{z}=\frac{y}{x}+\frac{z}{x}+\frac{x}{y}+\frac{z}{y}+\frac{x}{z}+\frac{y}{z}\)
\(=\left(\frac{y}{x}+\frac{y}{z}\right)+\left(\frac{x}{y}+\frac{x}{z}\right)+\left(\frac{z}{x}+\frac{z}{y}\right)=y\left(\frac{1}{x}+\frac{1}{z}\right)+x\left(\frac{1}{y}+\frac{1}{z}\right)+z\left(\frac{1}{x}+\frac{1}{y}\right)\)
\(=y\cdot-\frac{1}{y}+x\cdot-\frac{1}{x}+z\cdot-\frac{1}{z}=-1-1-1=-3\)
vậy A=-3
Đúng 0
Bình luận (0)
cho x,y,z khác 0 và x-y-z=0, tính giá trị của biểu thức B=(1-z/x) (1-x/y) (1+y/z)
x-y-z=0
=> x=y+z
y=x-z
-z=y-x
B=(1-z/x)(1-x/y)(1+y/z)
B=((x-z)/x)((y-x)/y)((z+y)/z)
B=(y/x)(-z/y)(x/z)
B=(-z.y.x)/(x.y.z)
B=-1
Đúng 6
Bình luận (0)
Xem thêm câu trả lời
cho x,y,z khác 0 và x-y-z=0 tính giá trị biểu thức b=( 1-z/x ) . ( 1-x/y ) . (1+x/y)
Cho x,y,z khác 0 và 1/x+1/y+1/z=0. Tính giá trị của biểu thức Q= x+y/z + y+x/x + z+x/y
Cho x,y,z khác 0 và x-y-z=0. Tính giá trị biểu thức A=(1-z/x)(1-x/y)(1+y/z)
\(A=\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)=\frac{\left(x-z\right)\left(y-x\right)\left(y+z\right)}{xyz}=\frac{y.\left(-z\right).x}{xyz}=-1\)
Cho x, y, z khác 0 và x - y - z = 0. Tính giá trị của biểu thức: B = (1 - z/x)(1 - x/y)(1 + y/x)
Cho x,y,z khác 0 và x-y-z=0,tính giá trị biểu thức
B= (1 - z/x) (1- x/y) (1+ y/z)
x - y - z = 0
x = y + z
y = x - z
z = x - y => -z = y - x
B = (1 - z/x)(1 - x/y) (1 + y/z)
B = (x/x - z/x)( y/y - x/y) ( z/z + y/z)
B = \(\frac{x-z}{x}\cdot\frac{y-x}{y}\cdot\frac{z+x}{z}=\frac{y}{x}\cdot\frac{-z}{y}\cdot\frac{x}{z}=-1\)
Đúng 2
Bình luận (0)

