cho parabol(p)y= ax2;
tìm a biết rằng (p) đi qua điểm k(2;4) vẽ đồ thị (p) với a vừa tìm được
PH
Những câu hỏi liên quan
TC
3 tháng 2 2021 lúc 16:18
Cho parabol (P): y=ax2(a khác 0) đi qua điểm A(2;4). Tìm trên parabol các điểm cách O một khoảng bằng \(\sqrt{5}\)
Xác định Parabol (P):
y
ax
2
+
bx
+
3
biết rằng Parabol có đỉnh I (3; -2) A.
y
x
2
−
6
x
+
3
B.
y
−
5
9
x
2
+
10
3
x
+
3
C. ...
Đọc tiếp
Xác định Parabol (P): y = ax 2 + bx + 3 biết rằng Parabol có đỉnh I (3; -2)
A. y = x 2 − 6 x + 3
B. y = − 5 9 x 2 + 10 3 x + 3
C. y = 3 x 2 + 9 x + 3
D. y = 5 9 x 2 − 10 3 x + 3
Chọn khẳng định đúng. Nếu phương trình
a
x
2
m
x
+
n
vô nghiệm thì đường thẳng d: y mx + n và parabol (P):
y
a
x
2
A. Cắt nhau tại hai điểm B. Tiếp xúc với nhau C. Không cắt nhau D. Cắt nhau tại gốc tọa độ
Đọc tiếp
Chọn khẳng định đúng. Nếu phương trình a x 2 = m x + n vô nghiệm thì đường thẳng d: y = mx + n và parabol (P): y = a x 2
A. Cắt nhau tại hai điểm
B. Tiếp xúc với nhau
C. Không cắt nhau
D. Cắt nhau tại gốc tọa độ
Đáp án C
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 không cắt nhau thì phương trình a x 2 = m x + n vô nghiệm.
Đúng 0
Bình luận (0)
Đường thẳng d: y mx + n và parabol (P):
y
a
x
2
(
a
≠
0
)
tiếp xúc với nhau khi phương trình
a
x
2
m
x
+
n
có: A. Hai nghiệm phân biệt B. Nghiệm kép C. Vô nghiệm D. Có hai nghiệm âm
Đọc tiếp
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 ( a ≠ 0 ) tiếp xúc với nhau khi phương trình a x 2 = m x + n có:
A. Hai nghiệm phân biệt
B. Nghiệm kép
C. Vô nghiệm
D. Có hai nghiệm âm
Đáp án B
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a x 2 = m x + n ⇔ a x 2 - m x - n = 0 có nghiệm kép ( Δ = 0 )
Đúng 0
Bình luận (0)
Tìm parabol (P): y ax2 + 3x – 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2. A. y x2 + 3x – 2. B. y -x2 + x – 2. C. y -x2 + 3x – 3. D. y -x2 + 3x – 2.
Đọc tiếp
Tìm parabol (P): y = ax2 + 3x – 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2.
A. y = x2 + 3x – 2.
B. y = -x2 + x – 2.
C. y = -x2 + 3x – 3.
D. y = -x2 + 3x – 2.
Vì parabol (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên A(2; 0) thuộc (P).
Thay x = 0; y = 2 vào phương trình parabol ta được 0 = 4a + 6 – 2 hay a = -1
Chọn D.
Đúng 0
Bình luận (0)
Chọn khẳng định đúng. Nếu phương trình
a
x
2
m
.
x
+
n
có hai nghiệm phân biệt thì đường thẳng d: y mx + n và parabol (P):
y
a
x
2
A. Cắt nhau tại hai điểm B. Tiếp xúc với nhau C. Không cắt nhau D. Cắt nhau tại gốc tọa độ
Đọc tiếp
Chọn khẳng định đúng. Nếu phương trình a x 2 = m . x + n có hai nghiệm phân biệt thì đường thẳng d: y = mx + n và parabol (P): y = a x 2
A. Cắt nhau tại hai điểm
B. Tiếp xúc với nhau
C. Không cắt nhau
D. Cắt nhau tại gốc tọa độ
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 cắt nhau tại hai điểm phân biệt khi phương trình a x 2 = m . x + n có hai nghiệm phân biệt.
Đáp án: A
Đúng 0
Bình luận (0)
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Có đỉnh là I(2; -2)
Parabol y = ax2 + bx + 2 có đỉnh I(2 ; –2), suy ra :
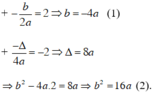
Từ (1) ⇒ b2 = 16.a2, thay vào (2) ta được 16a2 = 16a ⇒ a = 1 ⇒ b = –4.
Vậy parabol cần tìm là y = x2 – 4x + 2.
Đúng 0
Bình luận (0)
cho parabol y=ax2+bx+3 có đỉnh I(2;-2) khi đó giá trị a+2b bằng
Xem chi tiết
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-4a\\12a-16a^2=-8a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=-4a\\a=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{4}\\b=-5\end{matrix}\right.\)
\(\Rightarrow a+2b=...\)
Đúng 1
Bình luận (0)
tìm parabol y=ax2+bx+3 biết rằng parabol đó có trục đối xứng là x=-2 và đỉnh của parabol có tung độ bằng 19.
Lời giải:
Theo bài ra thì tọa độ đỉnh của parabol là $(-2,19)$
Từ hàm $y=ax^2+bx+3=a(x+\frac{b}{2a})^2+3-\frac{b^2}{4a}$ ta có tọa độ đỉnh của parabol là:
$(\frac{-b}{2a}, 3-\frac{b^2}{4a})$
$\Rightarrow \frac{-b}{2a}=-2; 3-\frac{b^2}{4a}=19$
$\Rightarrow a=-4; b=-16$
Đúng 3
Bình luận (0)
Xác định Parabol (P):
y
ax
2
+
b
x
−
5
biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x
-
3
2
A.
y
1
18
x
2
+
1
6
x
−
5
B.
y
1...
Đọc tiếp
Xác định Parabol (P): y = ax 2 + b x − 5 biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x = - 3 2
A. y = 1 18 x 2 + 1 6 x − 5
B. y = 1 18 x 2 + 1 6 x + 5
C. y = 3 x 2 + 9 x − 9
D. y = − 1 18 x 2 + 1 6 x − 5
