cho hình vẽ bên chứng minh tam giác abc bằng tam giác adc và adab
Đọc tiếp
cho hình vẽ bên chứng minh tam giác abc bằng tam giác adc và ad=ab
ND
Những câu hỏi liên quan
Cho tam giác ABC, trên nửa mặt phẳng bờ AC không chứa điểm B vẽ đoạn AD//BC và AD=BC. a/Chứng minh tam giác ADC bằng tam giác CBA, suy ra AB//CD. b/Gọi H;O;K lần lượt là trung điểm của AB;AC;CD. Chứng minh tam giác AOH bằng tam giác COK. c/Chứng minh O là trung điểm của HK
Cho tam giác ABC có AB bằng AC Gọi D là trung điểm của BC A)chứng minh tam giác ADB bằng tam giác ADC B)Chứng minh AD là phân giác của tam giác ABC C)vẽ DM vuông góc với AB(M thuộc AB) DN vuông góc với AC (N thuộc AC) Chứng minh rằng tam giác ADM bằng tam giác AND và MN//BC
a: Xét ΔADB và ΔADC có
AB=AC
AD chung
BD=CD
Do đó: ΔADB=ΔADC
b: Ta có: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
c: Xét ΔADM vuông tại M và ΔADN vuông tại N có
AD chung
\(\widehat{DAM}=\widehat{DAN}\)
Do đó: ΔADM=ΔADN
=>AM=AN
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Đúng 0
Bình luận (0)
Cho hình vuông ABCD ( hình vẽ bên) có AB = 20 cm AD = 30 cm DC = 40 cm Nối A với C được hình tam giác mà ABC và hình ADC tính A diện tích mỗi hình tam giác đó b tính tỉ số phần trăm của diện tích hình tam giác ABC và điểm ADC
cho tam giác abc có ab =ac . vẽ ad vuông góc ab sao cho ad =ab ( d khác phía đối với ab ) , vẽ ae vuông góc ac sao cho ae = ac ( e khác phía b đối vớiac )
a )chứng minh : tam giác BAD=tam giác CAE ; tam giác ADC =tam giác ABE và BDC =tam giác CEB
b)chứng minh CD vuộng góc BE
Cho tam giác ABC cân tại a.Điểm D là trung điểm của BC a) chứng minh tam giác ADB bằng tam giác ADC b) vẽ BE vuông góc với AC (E thuộc AC).Gọi F là giao điểm của AD và BE chứng minh đường thẳng CF vuông góc AB
Câu 1: Vẽ phân giác AD của tam giác ABC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a, Chứng minh: BD = DE
b, Gọi K là giao điểm của các đường thẳng AB và ED. Chứng minh: tam giác DBK = tam giác DEC và tam giác ADC = tam giác ADK
c, Chứng minh AD là đường trung trực của BE
giúp tui với mọi người ơi
Lười đánh máy thật sự:vvv
a) Xét ∆ABD và ∆AED:
AD: cạnh chung
AB=AE(gt)
\(\widehat{BAD}=\widehat{CAD}\) (AD là phân giác góc BAC)
=> ∆ABD=∆AED (c.g.c)
=> BD=DC
b) Theo câu a: ∆ABD=∆AED
=> \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{DBK}=180^o\\\widehat{AED}+\widehat{DEC}=180^o\end{matrix}\right.\)
\(\Rightarrow\widehat{DBK}=\widehat{DEC}\)
Xét ∆DBK và ∆DEC:
BD=ED(cm ở a)
\(\widehat{DBK}=\widehat{DEC}\left(cmt\right)\)
\(\widehat{BDK}=\widehat{EDC}\) ( 2 góc đối đỉnh)
=> ∆DBK=∆DEC (g.c.g)
c) Gọi giao điểm của AD và BE là I
Xét ∆BAI và ∆EAI:
AB=AE(gt)
\(\widehat{BAI}=\widehat{EAI}\left(gt\right)\)
AI: cạnh chung
=> ∆BAI=∆EAI (c.g.c)
=> \(\left\{{}\begin{matrix}BI=EI\left(1\right)\\\widehat{AIB}=\widehat{AIE}\end{matrix}\right.\)
Mà \(\widehat{AIB}+\widehat{AIE}=180^o\) (2 góc kề bù)
=> \(\widehat{AIB}=\widehat{AIE}=90^o\left(2\right)\)
Từ (1) và (2) suy ra AD là trung trực của BE.
Đúng 1
Bình luận (0)
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AE chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)
Đúng 1
Bình luận (0)
Tam giác ABC vuông tại A (AB < AC). Vẽ đường cao AH. Lấy D đối xứng với B qua H.
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA
b) Qua C vẽ đường thẳng vuông góc với tia AD cắt AD tại E. Chứng minh rằng AH.CD = CE.AD
c) Chứng minh tam giác HDE đồng dạng với tam giác ADC.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích tam giác DEC
e) AH cắt CE tại F. Chứng minh ABFD là hình thoi.
Cho hình thang ABCD ( AB//CD ), AB < CD và đường chéo AC vuông hóc với cạnh bên AD, đường cao AH a ) Chứng minh tam giác ADC đôngg dạng tam giác HAC b ) Chứng minh AC.AD = AH. CD c ) Cho biết AB = 14cm ; AC = 16cm và AD 12cm. Tính độ dài các đoạn Hd, HC và diện tích honhf thang ABCD
a: Xét ΔADC vuông tại A và ΔHAC vuông tại H có
góc ACD chung
=>ΔADC đồng dạng với ΔHAC
b: S ACD=1/2*AC*AD=1/2*AH*CD
=>AC*AD=AH*CD
c: CD=căn 12^2+16^2=20cm
HD=12^2/20=144/20=7,2cm
HC=20-7,2=12,8cm
Đúng 0
Bình luận (0)
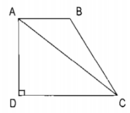
Cho hình thang vuông ABCD (xem hình vẽ) có AB = 20cm, AD = 30cm, DC = 40cm.
Nối A với C được hai hình tam giác là ABC và ADC. Tính :
a. Diện tích mỗi hình tam giác đó.
b. Tỉ số phần trăm của diện tích hình tam giác ABC và hình tam giác ADC.
a. Diện tích hình thang ABCD là :
(
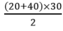=900
(
c
m
2
)
Diện tích tam giác ADC là :
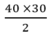=600
(
c
m
2
)
Diện tích tam giác ABC là :
900 – 600 = 300 ( c m 2 )
b. Tỉ số phần trăm của diện tích tam giác ABC và hình tam giác ADC là :
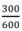×100 = 50%
Đáp số:
a. Diện tích tam giác ABC : 300 ( c m 2 )
Diện tích tam giác ADC : 600 ( c m 2 )
b. %SABC = 50%
Đúng 0
Bình luận (0)