Mn vẽ giúp hình vs ạ
KL
Những câu hỏi liên quan
Mn ơi, giúp e vs ạ, em cảm tạ
Vẽ hình nữa nha mn

M là trung điểm AB, MK song song BC.
\(\Rightarrow\) MK đi qua trung điểm AI.
hay K là trung điểm AI.
Đúng 1
Bình luận (0)
Mn ơi giúp em bài này vs ạ  Vẽ cả hình nx
Vẽ cả hình nx
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
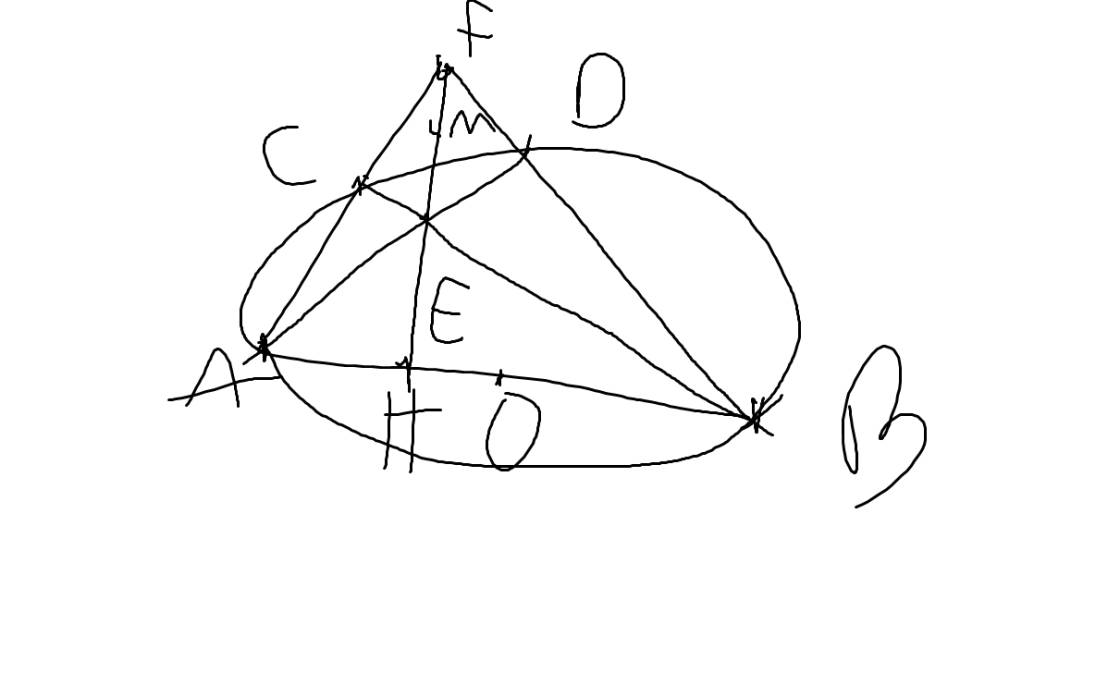
Đúng 2
Bình luận (0)
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
Cho hình thang cân ABCD có đáy nhỏ AB. Vẽ AH vuông góc với CD. CMR: CH=\(\dfrac{CD+AB}{2}\). mn giúp mình vs ạ, mình đang cần gấp ạ. <33 Thanks mn nhiều.
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Đúng 1
Bình luận (0)
BÀI 1.Cho đường tròn(O,13cm). Dây cungAB. GọiMlà trung điểm củaAB. BiếtOM=5cm, tính độ dài dây cungAB. mn giúp vs và vẽ hình đc ko ạ
Xét ΔAMO vuông tại M có
\(OA^2=AM^2+OM^2\)
\(\Leftrightarrow AM=12\left(cm\right)\)
hay AB=24(cm)
Đúng 0
Bình luận (0)
góc nội tiếp là góc vuông thì chắn nửa đường tròn là đúng hay sai, vẽ hình minh họa và giải thích
*mn ơi mn ơi giúp mình vs ạ
giúp e vs. vẽ giúp e hình vs ạ
a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
Đúng 1
Bình luận (0)
mn giúp mik vs ạ, phải đúng chuẩn và đủ nha ạ, bài hình thì phải có hình ạ


\(11,\\ a,=4\cdot5+14:7=20+2=22\\ b,=3\sqrt{2}-12\sqrt{2}+5\sqrt{2}=-4\sqrt{2}\\ c,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)}=\dfrac{6}{7}\\ 12,\\ a,P=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ P=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ b,P=\dfrac{1}{2}\Leftrightarrow\sqrt{x}+3=4\Leftrightarrow x=1\left(tm\right)\)
Đúng 4
Bình luận (0)
a: \(=4\cdot5+14:7=20+2=22\)
b: \(=3\sqrt{2}-8\sqrt{2}+5\sqrt{2}=0\)
Đúng 1
Bình luận (0)
\(14,\\ ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{\left(x-1\right)\left(x-2\right)}+\sqrt{x+3}=\sqrt{x-2}+\sqrt{\left(x+3\right)\left(x-1\right)}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x-1}=a\\\sqrt{x-2}=b\\\sqrt{x+3}=c\end{matrix}\right.\left(a,b,c\ge0\right)\), PTTT:
\(ab+c=b+ac\\ \Leftrightarrow a\left(b-c\right)-\left(b-c\right)=0\\ \Leftrightarrow\left(a-1\right)\left(b-c\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\b=c\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-2=x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\0x=5\left(ktm\right)\end{matrix}\right.\\ \Leftrightarrow x=2\)
Đúng 3
Bình luận (1)
Xem thêm câu trả lời



