Tìm điều kiện của x để giá trị của biểu thức
được xác định.
Tính giá trị của biểu thức tại x = 20040.
Tìm điều kiện của x để giá trị của biểu thức
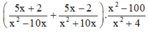
được xác định.
Tính giá trị của biểu thức tại x = 20040.
+ Tìm điều kiện xác định:
Biểu thức xác định khi tất cả các phân thức đều xác định.
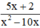 xác định ⇔ x2 – 10x ≠ 0
xác định ⇔ x2 – 10x ≠ 0
⇔ x(x – 10) ≠ 0
⇔ x ≠ 0 và x – 10 ≠ 0
⇔ x ≠ 0 và x ≠ 10
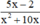 xác định ⇔ x2 + 10x ≠ 0
xác định ⇔ x2 + 10x ≠ 0
⇔ x(x + 10) ≠ 0
⇔ x ≠ 0 và x + 10 ≠ 0
⇔ x ≠ 0 và x ≠ -10
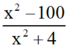 luôn xác định vì x2 + 4 > 0 với mọi x ∈ R.
luôn xác định vì x2 + 4 > 0 với mọi x ∈ R.
Vậy điều kiện xác định của biểu thức là x ≠ 0 và x ≠ ±10
+ Rút gọn biểu thức:
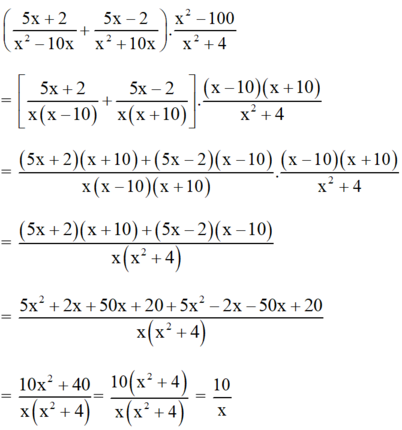
+ Tại x = 20040, giá trị biểu thức bằng 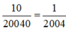
a) Tìm điều kiện của biến x để giá trị của biểu thức xác định. b) Tính giá trị của biểu thức với x=20040
a: ĐKXĐ: \(x\notin\left\{0;10;-10\right\}\)
Tìm điều kiện của x để giá trị của biểu thức :
\(\left(\dfrac{5x+2}{x^2-10x}+\dfrac{5x-2}{x^2+10x}\right).\dfrac{x^2-100}{x^2+4}\)
được xác định. Tính giá trị của biểu thức tại \(x=20040\)
khi
Hay
khi
Hay
Vậy điều kiện của biến x để biểu thức đã cho được xác định là
Để việc tính giá trị của biểu thức được đơn giản hơn ta rút gọn biểu thức trước :
=
ĐKXĐ: x2 - 10x khác 0, x2 + 10x khác 0
<=> x khác 0 và x khác +-10.
\((\dfrac{5x + 2}{x^2-10x}+\dfrac{5x-2}{x^2+10x}).\dfrac{x^2-100}{x^2+4}\)
= \(\dfrac{(5x+2)(x+10)+(5x-2)(x-10)}{x(x-10)(x+10)} .\dfrac{(x-10)(x+10)}{x^2+4}\)
= \(\dfrac{5x^2+12x+20+5x^2-12x+20}{x(x^2+4)}\)
= \(\dfrac{10x^2+40}{x(x^2+4)}\)
= \(\dfrac{10(x^2-4)}{x(x^2-4)}\)
= \(\dfrac{10}{x}\)
Thay x = 20040 vào biểu thức, ta có:
\(\dfrac{10}{20040}\) = \(\dfrac{1}{2004}\)
A=x^2+2x/2x+10 + x-5/x + 50x-5x/2x(x+5)
a)Tìm điều kiện của biến để giá trị của biểu thức được xác định
b)Tìm x để giá trị biểu thức bằng 1
c)Tính giá trị của biểu thức tại x=-3,x=-5
a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
Cho biểu thức
1 3 1
. 1 1 2
x x x A
x x
1) Tìm điều kiện của x để biểu thức A được xác định. 2) Rút gọn biểu thức A. 3) Tính giá trị của biểu thức A tại x 5. 4) Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)
Cho biểu thức: P = x 2 + 2 x 2 x + 12 + x − 6 x + 108 − 6 x 2 x ( x + 6 ) .
a) Tìm điều kiện của biến x để giá trị của biểu thức đuợc xác định;
b) Rút gọn phân thức;
c) Tìm giá trị của x để giá trị của biểu thức bằng 3 2
d) Tìm giá trị của x để giá trị của biểu thức bằng - 9 2
e) Tìm giá trị của x để giá trị của biểu thức bằng 1.
a) Tìm được x ≠ -6 và x ≠ 0.
b) Gợi ý: x 3 + 4 x 2 - 6x + 36 = (x + 6) ( x 2 - 2x + 6)
Tìm được P = x 2 − 2 x + 6 2 x
c) Ta có P = 3 2 ⇔ x 2 − 5 x + 6 = 0 . Từ đó tìm được x = 2 hoặc x = 3 (TMĐK).
d) Tương tự câu c, tìm được x = -6 (KTM) hoặc x = -1 (TM)
e) P = 1 Þ x 2 ‑ - 4x + 6= 0 Û ( x - 2 ) 2 + 2 = 0 (vô nghiệm)
Vì ( x - 2 ) 2 + 2 ≥ 2 > 0 với mọi x. Do vậy x ∈ ∅ .
Cho \(A=\left(\frac{5x+2}{x^2-10x}+\frac{5x-2}{x^2+10x}\right).\frac{x^2-100}{x^2+4}\)
a) Tìm điều kiện của x để biểu thức xác định
b) Tính giá trị của A tại x=20040
a) ĐKXĐ:
x2-10x khác 0 và x2+10x khác 0
=>x.(x-10) khác 0 và x.(x+1) khác 0
=>x khác 0 và x khác 10 ;-10
b)\(A=\left(\frac{5x+2}{x^2-10x}+\frac{5x-2}{x^2+10x}\right).\frac{x^2-100}{x^2+4}\)
\(=\frac{5x+2}{x^2-10x}.\frac{x^2-100}{x^2+4}+\frac{5x-2}{x^2+10x}.\frac{x^2-100}{x^2+4}\)
\(=\frac{5x+2}{x.\left(x-10\right)}.\frac{\left(x-10\right)\left(x+10\right)}{x^2+4}+\frac{5x-2}{x.\left(x+10\right)}.\frac{\left(x-10\right)\left(x+10\right)}{x^2+4}\)
\(=\frac{\left(5x+2\right).\left(x+10\right)}{x.\left(x^2+4\right)}+\frac{\left(5x-2\right).\left(x-10\right)}{x.\left(x^2+4\right)}\)
\(=\frac{5x^2+52x+20+5x^2-52x+20}{x.\left(x^2+4\right)}=\frac{10x^2+40}{x.\left(x^2+4\right)}=\frac{10.\left(x^2+4\right)}{x.\left(x^2+4\right)}=\frac{10}{x}\)
Để A=20040 thì:
10/x=20040
=>x=1/2004
Cho A=\(\hept{\begin{cases}5X^2+2\\X-10\end{cases}+\frac{5X-2}{X+10}.\frac{X^2-100}{X^2+4}}\)
A,TÌm điều kiện của x để biểu thức A xác định
b,Tính giá trị của A tại x=20040
1.Cho biểu thức C = x³/x²-4 - x/x-2 - 2/x+2
a,tìm giá trị của biến để biểu thức được xác định
b,Tìm x để C=0
c,Tìm giá trị nguyên của x để C nhận giá trị dương
2,cho P = (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³
a,Tìm điều kiện của x để giá trị của P được xác định
B, rút gọn P
c,Tính giá trị P với |x-5|=2
d,Tìm x để P<0
3,cho biểu thức B = [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5
a,Tìm điều kiện của x để giá trị biểu thức được xác định
b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?
4,Cho phân thức C = 3x²-x/9x²-6x+1
a, tìm điều kiện xác định phân thức
b,tính giá trị phân thức tại x=-8
c,Tìm x để giá trị của phân thức nhận giá trị dương
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
chết mk nhìn nhầm phần c bài 2 :
\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)
Để P xác định
\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)
\(2+x\ne0\Rightarrow x\ne-2\)
\(x^2-4\ne0\Rightarrow x\ne0\)
\(x^2-3x\ne0\Rightarrow x\ne3\)
b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)
\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)
\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)
d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)
\(TH1:8x^2-4x^3< 0\)
\(\Rightarrow8x^2< 4x^3\)
\(\Rightarrow2< x\Rightarrow x>2\)
\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)