Vẽ hình + ghi gt kl dùm mik với đnag cần gấp ạ
H24
Những câu hỏi liên quan
dùm mình gấp bài này với ạ ( viết luôn cả gt-kl, vẽ luôn hình )

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=3.6\left(cm\right)\)
CH=BC-BH=6,4(cm)
Đúng 0
Bình luận (0)
Trên hình vẽ sau có các tam giác nào bằng nhau? Vì sao?
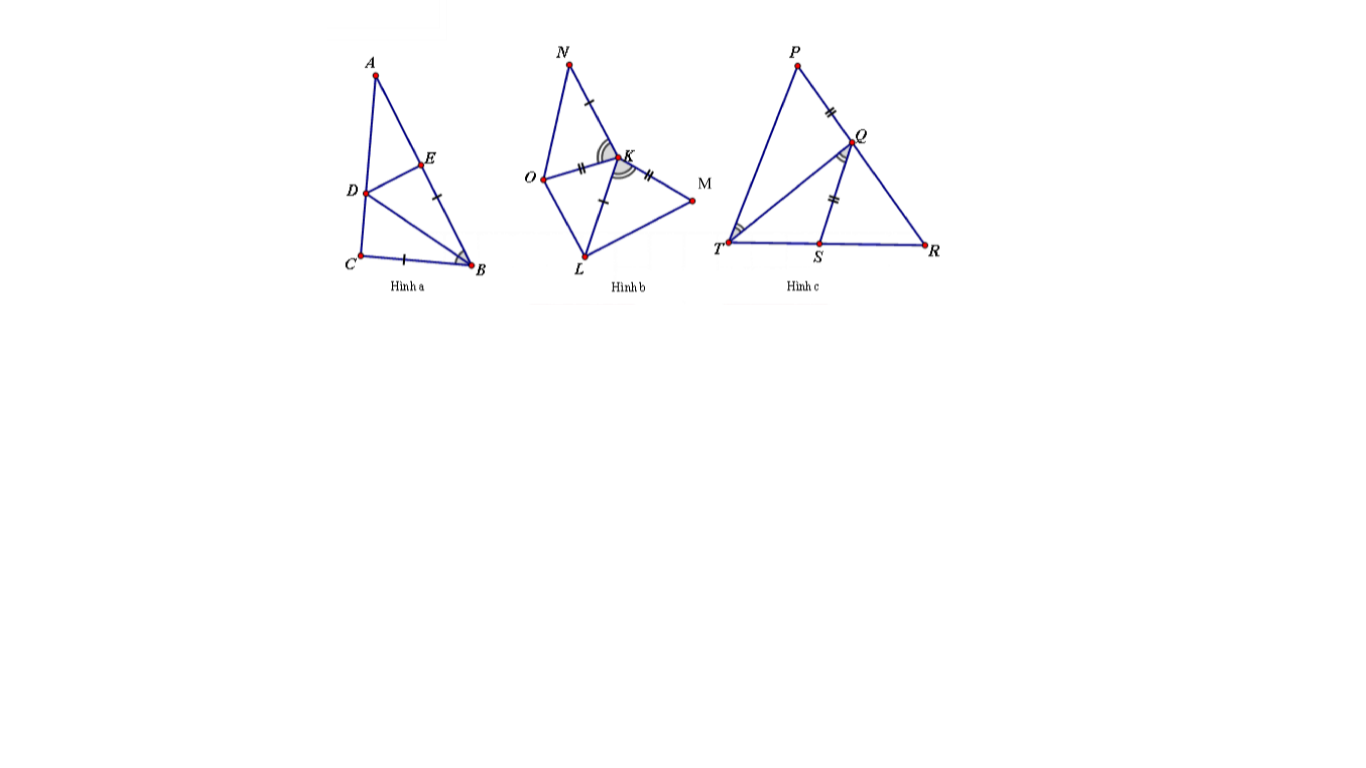
(Vẽ hình và ghi GT -KL)
Mình đang cần gấp
Biết 2 cạnh của hình chữ nhật với tỷ lệ 4 và 4 . Diện tihs hình chữ nhật bằng 500 m². Tính các kích thước của hình chữ nhật đó ?
Giups mik với ạ . Mik đnag cần gấp . Mik sẽ tick hết
đây nha bạn
Gọi a(m)a(m) là chiều dài hình chữ nhật (a,b>0)(a,b>0)
b(m)b(m) là chiều rộng hình chữ nhật
Diện tích hình chữ nhật là: a.b=500(m)a.b=500(m)
Vì 22 cạnh của hình chữ nhật tỉ lệ với 44 và 55 nên ba=45ba=45
Ta có:⎧⎨⎩a.b=500ba=45⇔{a.b=5005b=4a⇔{a=500:b5b=4.500b⇔{a=500:b5b2=2000⇔{a=500:bb2=400⇔⎧⎪⎨⎪⎩a=25(N)[b=20(N)b=−20(L){a.b=500ba=45⇔{a.b=5005b=4a⇔{a=500:b5b=4.500b⇔{a=500:b5b2=2000⇔{a=500:bb2=400⇔{a=25(N)[b=20(N)b=−20(L)
Vậy chiều dài hình chữ nhật là 25m25m
Chiều rộng hình chữ nhật là 20m
Cho ∆ABC cân tại A. Trên nửa mặt phẳng bờ BC không chứa điểm A, vẽ tia Bx//AC và trên tia này lấy điểm M sao cho BM = BA. Chứng minh: a. AM vuông BC b. ∆MBC cân Mong mụi ngừ giúp mik giải bt này ạ... Nhớ vẽ hình với ghi GT, KL giùm mik ạ, plsss 🙏😖
a) ∆ ABC cân tại A (gt). \(\Rightarrow\) AB = AC (Tính chất tam giác cân).
Mà AB = BM (gt).
\(\Rightarrow\) AB = AC = BM.
Xét tứ giác ACMB:
BM = AC (cmt).
BM // AC (Bx // AC).
\(\Rightarrow\) Tứ giác ACBM là hình bình hành (dhnb).
Mà AB = BM (gt).
\(\Rightarrow\) Tứ giác ACBM là hình thoi (dhnb).
\(\Rightarrow\) \(AM\perp BC\) (Tính chất hình thoi).
b) Xét ∆ MBC:
MB = MC (Tứ giác ACBM là hình thoi).
\(\Rightarrow\) ∆ MBC cân tại M.
Đúng 1
Bình luận (0)
vẽ hình dùm mình với ạ. Mình cần gấp
Đọc tiếp
vẽ hình dùm mình với ạ. Mình cần gấp

Vẽ dùm e cái hình luôn với ạ đang cần gấp😅
a)
Δ\(ABD\) có \(AM\) là tia phân giác của \(\widehat{ADB}\) \(\left(M\in AB\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{DA}{DB}\) (1)
b)
Δ\(ACD\) có \(AN\) là tia phân giác của \(\widehat{ADC}\) \(\left(N\in AC\right)\)
⇒ \(\dfrac{NA}{NC}=\dfrac{DA}{DC}\) (2)
Từ \(\left(1\right)và\left(2\right)\), mà \(BD=CD\left(gt\right)\)
⇒ \(\dfrac{MA}{MB}=\dfrac{NA}{NC}\)
⇒ \(MN\) // \(BC\) \(\left(ĐPCM\right)\)
c)
Δ\(ABC\) có \(MN\) // \(BC\) nên:
⇒ \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
⇒ \(AM.AC=AN.AB\)
Ta có: \(MN\) //\(BC\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_1}\\\widehat{N_1}=\widehat{D_4}\end{matrix}\right.\)
\(Mà\) \(\left\{{}\begin{matrix}\widehat{D_1}=\widehat{D_2}\\\widehat{D_3}=\widehat{D_4}\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}\widehat{M_1}=\widehat{D_2}\\\widehat{N_1}=\widehat{D_3}\end{matrix}\right.\)
Δ\(MKD\) có \(\widehat{M_1}=\widehat{D_2}\) ⇒ \(\text{Δ}MKD\) cân tại K
⇒ \(MK=KD\) \(\left(3\right)\)
Δ\(NKD\) có \(\widehat{N_1}=\widehat{D_3}\) ⇒ \(\text{Δ }NKD\) cân tại K
⇒ \(KN=KD\) \(\left(4\right)\)
Từ (3) và (4) ⇒ \(MK=KN\)
hay K là trung điểm của MN
Đúng 2
Bình luận (0)
 cho mik GT,KL với ạ,( ko cần giải ạ)
cho mik GT,KL với ạ,( ko cần giải ạ)
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Đường cao AH = 10cm ; đường cao BK = 12cm. Tính độ dài các cạnh của tam giác ABC
Cần khá gấp (k cần vẽ hình, ghi gt kl đâu)
ta có:
AH.BC = BK.AC
10.BC = 12.AC
=>BC= 6.AC/5 => BC^2=36.AC^2/25
mặt khác:
AC^2 = AH^2 + BC^2/4 = AH^2 + 36.AC^2/100
=>(1-36/100). AC^2= AH^2 = 100
=> AC^2 = 100^2/8^2
=> AC = 100/8 = 25/2
=> BC = 6.25/2.5=15
Đúng 0
Bình luận (0)
ta có:
AH.BC = BK.AC
10.BC = 12.AC
=>BC= 6.AC/5 => BC^2=36.AC^2/25
mặt khác:
AC^2 = AH^2 + BC^2/4 = AH^2 + 36.AC^2/100
=>(1-36/100). AC^2= AH^2 = 100
=> AC^2 = 100^2/8^2
=> AC = 100/8 = 25/2
=> BC = 6.25/2.5=15
k mk nha
Làm ơn đó
Đúng 0
Bình luận (0)
ta có:
AH.BC = BK.AC
10.BC = 12.AC
=>BC= 6.AC/5 => BC^2=36.AC^2/25
mặt khác:
AC^2 = AH^2 + BC^2/4 = AH^2 + 36.AC^2/100
=>(1-36/100). AC^2= AH^2 = 100
=> AC^2 = 100^2/8^2
=> AC = 100/8 = 25/2
=> BC = 6.25/2.5=15
Đúng 0
Bình luận (0)
Giúp mik với mik đnag cần gấp





