Giúp mình với mn ơi,mình cần gấp
WY
Những câu hỏi liên quan
mn ơi giúp mình với ạ, mình cần gấp,mình cảm ơn mn
Giúp mình với mn ơi mình cần gấp

mn ơi giúp mình với ! (mình cần gấp :() 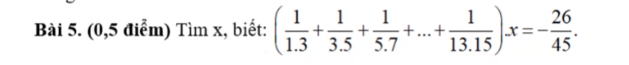
\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{13.15}\right).x=\dfrac{-26}{45}\\ \Leftrightarrow\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{13.15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{13}-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\left(1-\dfrac{1}{15}\right).x=\dfrac{-52}{45}\\ \Leftrightarrow\dfrac{14}{15}.x=\dfrac{-52}{45}\\ \Leftrightarrow x=-\dfrac{26}{21}\)
Đúng 1
Bình luận (0)
(11.3+13.5+...+113.15).x=−2645⇔(21.3+23.5+...+213.15).x=−5245⇔(1−13+13−15+...+113−115).x=−5245⇔(1−115).x=−5245⇔1415.x=−5245⇔x=−2621
Đúng 1
Bình luận (0)
Giúp mình với mn ơi , mình cần gấp!
giúp mình với mn ơi , mình cần gấp lắm
Mn ơi giúp mình với mình cần gấp ạ 
\(a,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ b,A=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{1;3\right\}\left(\sqrt{x}+1\ge1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2\right\}\\ \Leftrightarrow x\in\left\{0;4\right\}\left(tm\right)\)
Đúng 1
Bình luận (0)
a) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(\Rightarrow A=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
Đúng 0
Bình luận (0)
Mn ơi giúp mình với mình đang cần gấp

1. that - because
2. that
3. that - who
4. That - so
5. Where - what - who
Đúng 0
Bình luận (0)
Mn ơi giúp mình với ạ mình cần gấp ạ
1 his illness, he cannot come
2 her busyness, she couldn't help us
3 his illness, he tries to go to school on time
4 the bad weather, we tried to finish the work on the road
5 the bad weather, we got to the station late
6 the old house, she liked it
7 not wearing any shoes, Carol ran outside to see what was happening
8 being afraid of flying, Fiona had to get on the plane
Đúng 2
Bình luận (0)
Giúp mình bài 2 với Mn ơi
Mình cần gấp!!! 
Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC
Đúng 0
Bình luận (0)






