Hình hơi mờ ráng giúp mình nha
TV
Những câu hỏi liên quan
 nhanh giúp mình với ạ ,thông cảm hình hơi mờ
nhanh giúp mình với ạ ,thông cảm hình hơi mờ
Câu trả lời của AN là sai bởi vì 21/56 rút gọn thành 3/8 và 3/8 viết được dưới dạng số thập phân hữu hạn bởi vì
8 khi phân tích ra thành thừa số nguyên tố chỉ chứa số 2, đồng nghĩa không chứa số nào khác 2 và 5
=>21/56 viết được dưới dạng số thập phân hữu hạn
Đúng 1
Bình luận (0)
Giúp mình với nhé(hình hơi nhỏ và mờ thông cảm)
Xem thêm câu trả lời
giải giúp mình với ạ(xin lỗi vì hình hơi mờ

Giúp mình với bạn mình cần gấp ngay trong tối nay anh hơi mờ nhìn cố nha tạ ơn ạ

Bài 1:
a) Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}\)=\(\dfrac{x+y}{2+3}\)=\(\dfrac{-15}{5}\)= -3
=> x= -3.2= -6; y= -3.3= -9.
b) Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{3}=\dfrac{y}{4}\)=\(\dfrac{x-y}{3-4}\)=\(\dfrac{12}{-1}\)= -12
=> x= -12.3= -36; y= -12.4= -48
c) 3x=7y=\(\dfrac{x}{7}=\dfrac{y}{3}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{y}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)
=> x= -4.7= -28; y= -4.3= -12
d) \(\dfrac{x}{y}=\dfrac{17}{13}=\dfrac{x}{17}=\dfrac{y}{13}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{x}{17}=\dfrac{y}{13}=\dfrac{x+y}{17+13}=\dfrac{-60}{30}=-2\)
=> x= -2.17= -34; y= -2.13= -26
e) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
=>x= 9= \(3^2\)= 3.4= 12; y= 16= \(4^2\)= 4.4= 16
Đúng 0
Bình luận (0)
Bài 2:
2x=3y=\(\dfrac{x}{3}=\dfrac{y}{2}\); 5y=7z=\(\dfrac{y}{7}=\dfrac{z}{5}\)
-> \(\dfrac{x}{3}=\dfrac{y}{2};\dfrac{y}{7}=\dfrac{z}{5}\) = \(\dfrac{x}{21}=\dfrac{y}{14};\dfrac{y}{14}=\dfrac{z}{10}\)=> \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\) = \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tích chất dãy tỉ số bằng nhau:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)=\(\dfrac{3x-7y+5z}{63-98+50}\)=\(\dfrac{30}{15}=2\)
=> x= 2.21= 42
=> y= 2.14= 28
=> z= 2.10= 20
Đúng 0
Bình luận (0)
các bạn giải giúp mình nha, đề hơi mờ vì chụp bằng camera của máy tính các bạn thông cảm 
Hơi mờ nhưng cố giúp em nha m.n
Hơi mờ nhưng cố gắng giúp em nha m.n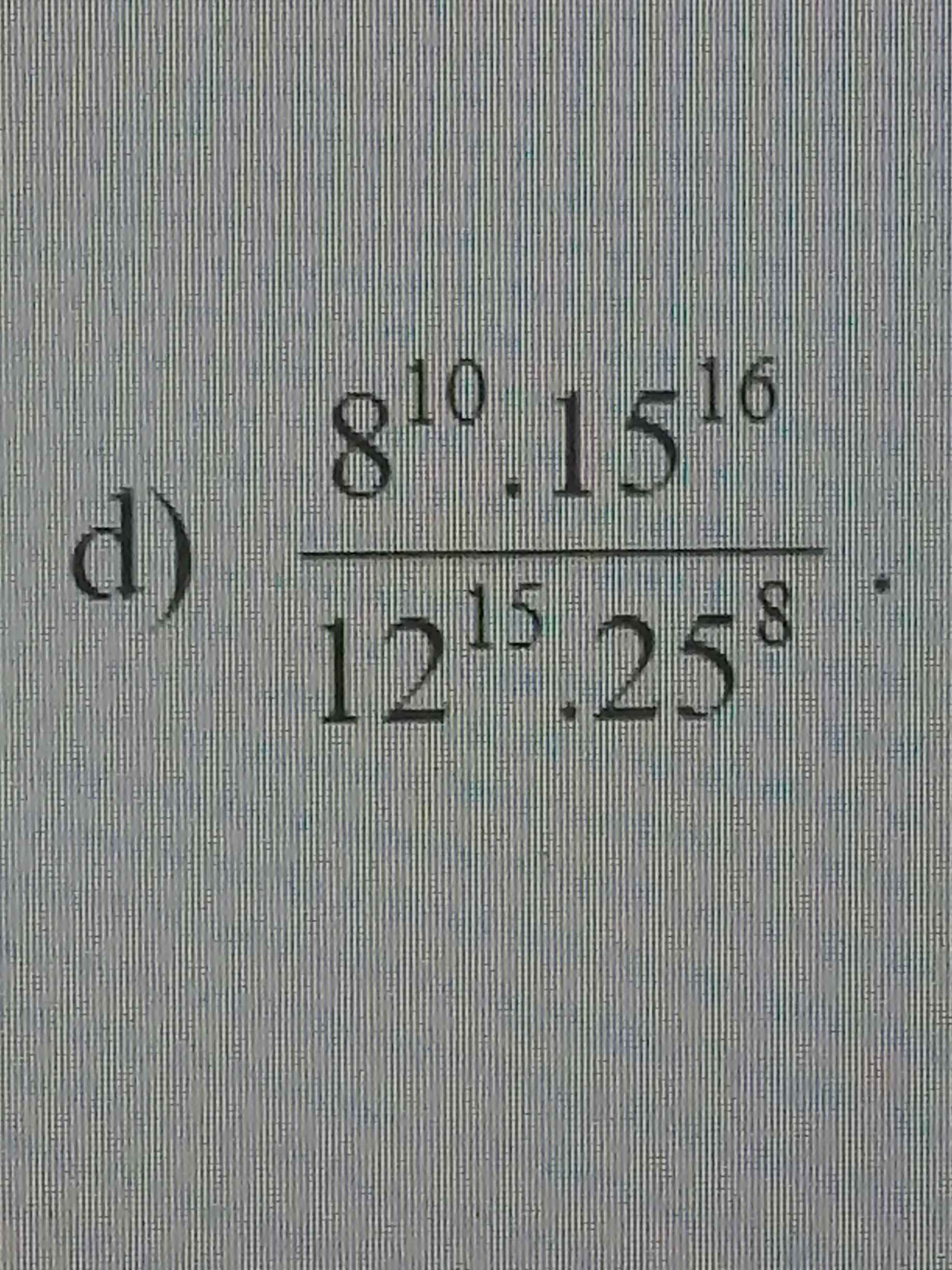
\(\dfrac{8^{10}.15^{16}}{12^{15}.25^8}\)
\(=\dfrac{\left(2.4\right)^{10}.\left(3.5\right)^{16}}{\left(3.4\right)^{15}.\left(5^2\right)^8}\)
\(=\dfrac{2^{10}.4^{10}.3^{16}.5^{16}}{3^{15}.4^{15}.5^{16}}\)
\(=\dfrac{2^{10}.3}{4^5}\)
\(=\dfrac{2^{10}.3}{2^{10}}=3\)
Đúng 2
Bình luận (1)
\(\dfrac{8^{10}.15^6}{12^{15}.25^8}\)
\(=\dfrac{\left(2.2.2\right)^{10}.\left(3.5\right)^{16}}{\left(3.2.2\right)^{15}.\left(5.5\right)^8}\)
\(=\dfrac{2^{10}.2^{10}.2^{10}.3^{16}.5^{16}}{3^{15}.2^{15}.2^{15}.5^8.5^8}\)
\(=\dfrac{3}{1}\)
\(=3\)
Đúng 0
Bình luận (0)
Máy mình chụp đề hơi mờ, các bạn thông cảm nha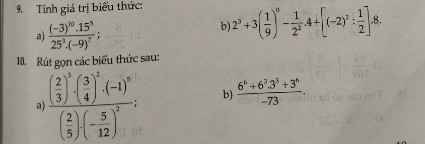
giúp mk vs!!!
Hơi mờ nên mọi người thông cảm nha

b)\(\sqrt{x^2-10x+25}=2x-3\) ĐK:x≥3/2
\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=2x-3\)
\(\Leftrightarrow\left|x-5\right|=2x-3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=2x-3\\x-5=3-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{8}{3}\end{matrix}\right.\)
Vậy phương trình có 2 nghiệm là ...
Đúng 1
Bình luận (1)
a: Ta có: \(\sqrt{25x+75}+3\sqrt{x-2}=2+4\sqrt{x+3}+\sqrt{9x-18}\)
\(\Leftrightarrow5\sqrt{x+3}-4\sqrt{x+3}=2\)
\(\Leftrightarrow x+3=4\)
hay x=1
Đúng 1
Bình luận (1)
c)ĐK:x≥1/2
\(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2x-1+2\sqrt{2x-1}+1}+\sqrt{2x-1-\sqrt{2x-1}+1}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{2x-1}+1\right)^2}+\sqrt{\left(\sqrt{2x-1}-1\right)^2}=2\)
\(\Leftrightarrow\left|\sqrt{2x-1}+1\right|+\left|\sqrt{2x-1}-1\right|=2\)
\(\Leftrightarrow\sqrt{2x-1}+1+\left|\sqrt{2x-1}-1\right|=2\) (do \(\sqrt{2x-1}+1\ge0\))
\(\Leftrightarrow\sqrt{2x-1}+1+\left|1-\sqrt{2x-1}\right|=2\)
Ta có:\(\sqrt{2x-1}+1+\left|1-\sqrt{2x-1}\right|\ge\sqrt{2x-1}+1+1-\sqrt{2x-1}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{2x-1}+1\right)\left(1-\sqrt{2x-1}\right)\ge0\)
\(\Leftrightarrow\dfrac{1}{2}\le x\le1\)
Vậy phương trình có tâp nghiệm \(S=\left\{x|\text{}\dfrac{1}{2}\le x\le1\right\}\)
Đúng 1
Bình luận (1)