Với giá trị nào m của thì phương trình có nghiệm kép:
\(x^2+\left(3-m\right)x-m-1=0\)
Với giá trị nào của m thì phương trình sau có nghiệm kép?
\(x^2-2\left(m-4\right)x+m^2+m+3=0\)
Cho phương trình :
\(\left(m+2\right)x^2+\left(2m+1\right)x+2=0\)
a) Xác định m để phương trình có hai nghiệm trái dấu và tổng hai nghiệm bằng -3
b) Với giá trị nào của m thì phương trình có nghiệm kép ? Tìm nghiệm kép đó ?
a) Để phương trình có hai nghiệm trái dấu khi và chỉ khi: \(ac< 0\Leftrightarrow2\left(m+2\right)< 0\)\(\Leftrightarrow m+2< 0\)\(\Leftrightarrow m< -2\). (1)
Tổng hai nghiệm đó bằng - 3 khi và chỉ khi:
\(x_1+x_2=\dfrac{2m+1}{m+2}=-3\)
\(\Rightarrow2m+1=3\left(m+2\right)\)\(\Leftrightarrow m=-5\)
Kết hợp với điều kiện (1) ta được \(m=-5\) là giá trị cần tìm.
b) Phương trình có nghiệm kép khi và chỉ khi:
\(\left\{{}\begin{matrix}a\ne0\\\Delta=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+2\ne0\\\left(2m+1\right)^2-4.2.\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\)
Vậy \(m=\dfrac{5}{2}\) hoặc \(m=-\dfrac{3}{2}\) là giá trị cần tìm.
1.Phương trình x^2 +5x -m -3 có nghiệm kép khi?
2.Cho pt x^2 - 5x+m-3 =0 (1)
1)Tìm m để pt có nghiệm kép. Tìm nghiệm kép đó.
2)Với giá trị nào của m thì phương trình (1) có 2 nghiệm phân biệt.
Giúp với ạ.
1.
xét delta có
25 -4(-m-3)
= 25 + 4m + 12
= 4m + 37
để phương trình có nghiệm kép thì delta = 0
=> 4m + 37 = 0 => m = \(\dfrac{-37}{4}\)
2.
a) xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có nghiệm kép thì delta = 0
=> -4m + 37 = 0
=> m = \(\dfrac{37}{4}\)
b)
xét delta
25 - 4(m-3) = 25 - 4m + 12 = -4m + 37
để phương trình có 2 nghiệm phân biệt thì delta > 0
=> -4m + 37 > 0
=> m < \(\dfrac{37}{4}\)
Cho phương trình
( m + 2 ) x 2 + ( 2 m + 1 ) x + 2 = 0
Với giá trị nào của m thì phương trình có nghiệm kép? Tìm nghiệm kép đó
Phương trình có nghiệm kép khi m ≠ -2 và Δ = 0.
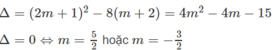
Khi m = 5/2 nghiệm kép của phương trình là
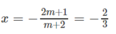
Khi m = -3/2 nghiệm kép của phương trình là x = 2.
1.Cho phương trình:\(\left(m+1\right)x^2-2\left(m+1\right)+m-3=0\)0
a)Với giá trị nào của m thì pt có nghiệm kép.Tính nghiệm kép
b)Với giá trị nào của m thì pt có nghiệm:\(x_1x_2\)
2.\(A=\frac{x}{x-4}+\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x+2}}\)
a)Rút gọn A
b)Tính x khi \(A=-\frac{1}{3}\)
Cho phương trình (ẩn x) x2 – 2(m – 1)x + m2 = 0
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 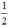
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 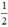
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 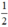
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 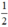 ; có nghiệm kép khi m =
; có nghiệm kép khi m = 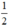 và vô nghiệm khi m >
và vô nghiệm khi m > 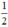
Với giá trị nào của m thì phương trình \(\left(m-1\right)x^2-2\left(m-2\right)x+m-3=0\) có hai nghiệm \(x_1,x_2\) thỏa mãn \(x_1+x_2+x_1x_2< 1\)?
Đoạn cuối mình làm sai:
\(\dfrac{3m-7}{m-1}< 1\Leftrightarrow\dfrac{2m-6}{m-1}< 0\Leftrightarrow1< m< 3\).
Nếu vậy thì đáp án đúng là A.
Để pt có 2 nghiệm thì:
\(\left\{{}\begin{matrix}m-1\ne0\\\Delta'=\left(m-2\right)^2-\left(m-3\right)\left(m-1\right)=1\ge0\end{matrix}\right.\Leftrightarrow m\ne1\).
Khi đó theo hệ thức Viète: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2\right)}{m-1}\\x_1x_2=\dfrac{m-3}{m-1}\end{matrix}\right.\).
Do đó \(x_1+x_2+x_1x_2< 1\Leftrightarrow\dfrac{2\left(m-2\right)+\left(m-3\right)}{m-1}< 1\Leftrightarrow\dfrac{3m-7}{m-1}< 1\Leftrightarrow3m-7< m-1\Leftrightarrow2m< 6\Leftrightarrow m< 3\).
Vậy m là các số thoả mãn m < 3 và m khác 1.
Với giá trị nào của m thì phương trình \(\left(m-1\right)x^2-2\left(m-2\right)x+m-3=0\) nghiệm thoả mãn \(x_1+x_2+x_1x_2< 1?\)
\(\Delta'=\left(m-2\right)^2-\left(m-1\right)\left(m-3\right)=1>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm với \(m\ne1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2\right)}{m-1}\\x_1x_2=\dfrac{m-3}{m-1}\end{matrix}\right.\)
\(x_1+x_2+x_1x_2< 1\)
\(\Leftrightarrow\dfrac{2\left(m-2\right)}{m-1}+\dfrac{m-3}{m-1}< 1\)
\(\Leftrightarrow\dfrac{3m-7}{m-1}-1< 0\)
\(\Leftrightarrow\dfrac{2m-6}{m-1}< 0\)
\(\Leftrightarrow1< m< 3\)
Điều kiện: m\(\ne\)1.
\(\Delta\)'=(m-2)2-(m-1)(m-3)=1>0.
x1+x2+x1x2=\(\dfrac{2\left(m-2\right)}{m-1}+\dfrac{m-3}{m-1}\)=\(\dfrac{3m-7}{m-1}\)<1 \(\Rightarrow\) 3m-7<m-1 \(\Rightarrow\) m<3.
Vậy với m\(\in\)(-\(\infty\);3)\{1}, yêu cầu bài toán thỏa mãn.
Cho phương trình: \(x^2-2\left(3m+2\right)x+2m^2-3m+5=0\)
a. Giải phương trình với m = -2
b. Tìm các giá trị của m để phương trình trên có một trong các nghiệm bằng 1
c. Tìm các giá trị của m để phương trình trên có nghiệm kép.