Tính diện tích tam giác ABC biết ba đường cao tam giác có độ dài lần lượt là 60cm,65cm,156cm
NA
Những câu hỏi liên quan
Tính diện tích tam giác ABC biết ba đường cao tam giác có độ dài lần lượt là 60cm ,65cm,156cm.
Tính diện tích tam giác ABC biết rằng 3 đường cao của tam giác đó có độ dài lần lượt là 60cm,65cm,156cm.
Gọi a là cạnh đối diện góc A, tương tự đối với b và c. Gọi chiều cao tương ứng với cạnh a là ha, tương tự đối với hb và hc. Ta có ha.a=hb.b=hc.c=2S, từ ha.a=hb.b => a/b=hb/ha=65/60=13/12 => đặt a=13k (k khác 0), b=12k (k khác 0). Từ hb.b=hc.c => b/c=hc/hb=156/65=12/5 => đặt c=5k (k khác 0), nhận thấy a;b và c thỏa mãn Pytago => theo định lý Pytago đảo thì tam giác ABC vuông tại A. Giả sử AH,BK,CL là đường cao từ các đỉnh. Theo hệ thức lượng trong tam giác vuông ta có AC^2=CH.BC <=> CH=(AC^2)/BC = 144k/13. Xét tam giác ACH có góc H=90 độ, nên áp dụng định lý Pytago ta có AH^2 + CH^2 = AC^2 => AC^2 - CH^2 = AH^2 <=> (12k)^2 - (144k/13)^2 = 60^2, sau đó ta tính được k=13 => AB=65mm; AC=156mm => diện tích ABC = (65 x 156 )/ 2 = 5070 mm^2
mình lớp 5 mong bạn thông cảm
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết rằng độ dài 3 đường cao tương ứng lần lượt là 60cm, 65cm, 156cm. Hãy tính diện tích hình tam giác ABC đó.
Muốn tính diện tích hình tam giác ta lấy các cạnh nhân lại với nhau
Vậy sẽ là bằng : 60 x 65 x 156 = 608400 (cm)
Đúng 0
Bình luận (0)
Tính diện tích tam giác ABC biết độ dài của ba đương cao tam giác ABC lần lượ là 60 cm,65cm,166cm
Tính diện tích tam giác biết ba đường cao có độ dài lần lượt là 60mm,56mm,156mm.
Tính diện tích tam giác ABC biết độ dài 3 đường cao lần lượt là 6; 6,5; 15,6.
Cho tam giác ABC biết độ dài ba đường cao lần lượt là 6 ,8 ,12 .tính độ dài ba cạnh của tam giác
hình như dựa vào tính chất dãy tỉ số bằng nhau ak pn. mk cx chỉ nhớ z thui chứ hk chắc cko lém :)
Đúng 0
Bình luận (0)
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
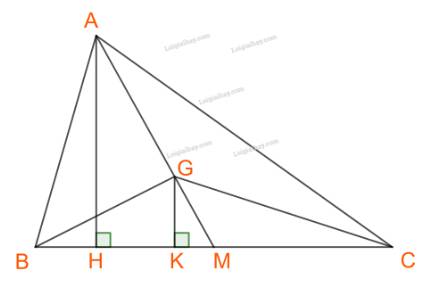
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)
Đúng 0
Bình luận (0)
Tính diện tích tam giác ABC biết răng 3 đường cao có độ dài lần lượt lad 60 ; 65 ; 156

