Bán kính đường tròn ngoại tiếp tam giác = 15cm

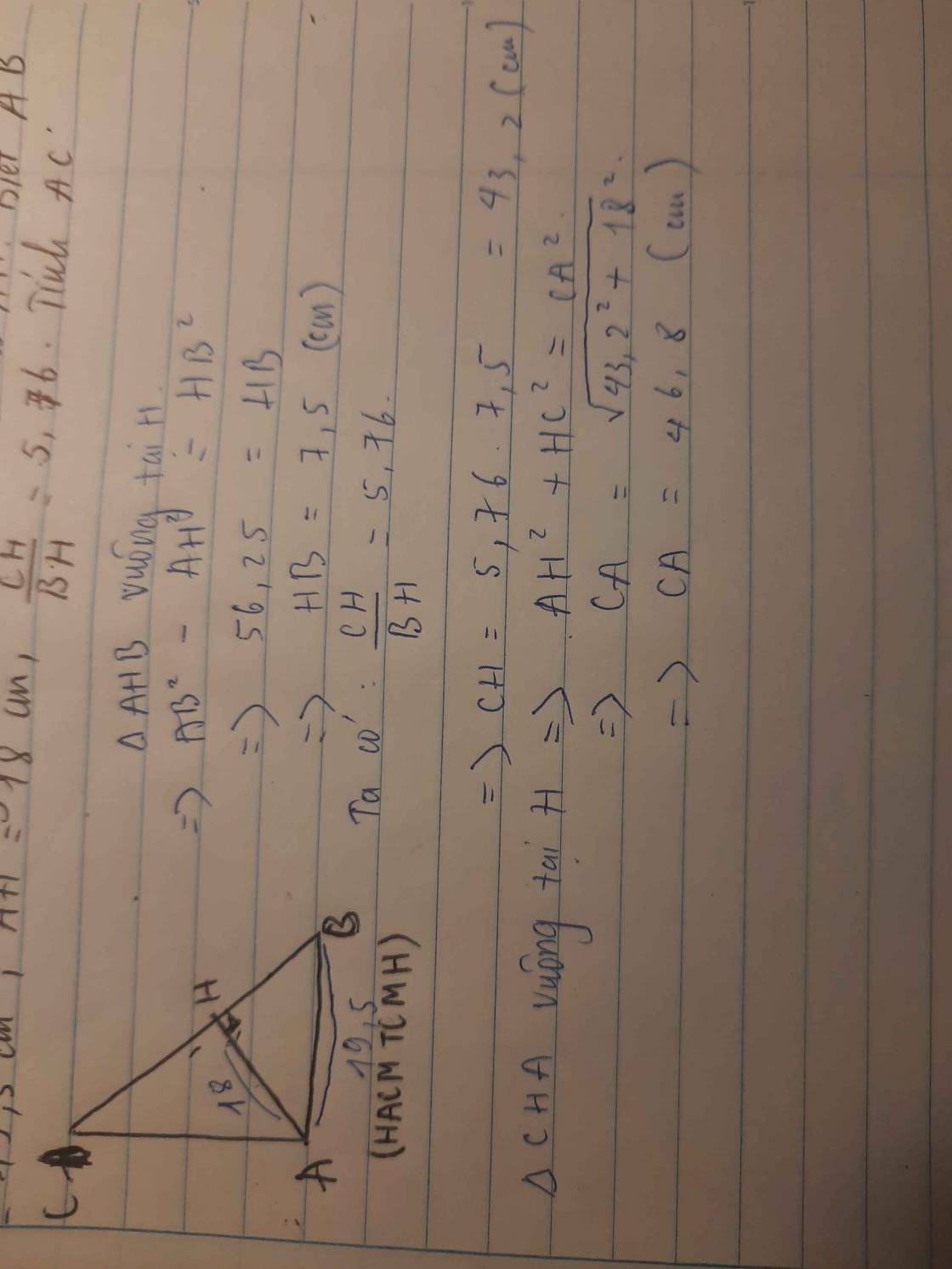  BC=BH+CH

       =7,5+43,2

       =50,7

CVabc= 50.7+19.5+46.8

Áp dụng định lý Py-ta-go vào tam giác ABC ta có:

\(AB^2+AC^2=BC^2\)

\(18^2+24^2=BC^2\)

\(324+576=BC^2\)

\(BC^2=900=30^2\)

\(\Rightarrow BC=30\left(cm\right)\)

chu vi tam giác ABC là 30+18+24=72(cm)

vậy ...

sao tính được

72 cm²

Tk mình nha mọi người!!!!

a) Ta có: \(\dfrac{AB}{BC}=\dfrac{4}{5}\)

nên \(AB=\dfrac{4}{5}BC\)

Xét ΔABC vuông tại A có 

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow BC=30\left(cm\right)\)

\(\Leftrightarrow AB=\dfrac{4}{5}\cdot BC=\dfrac{4}{5}\cdot30=24\left(cm\right)\)

Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)

hay \(\dfrac{AD}{24}=\dfrac{CD}{30}\)

mà AD+CD=AC=18cm(gt)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{24}=\dfrac{CD}{30}=\dfrac{AD+CD}{24+30}=\dfrac{18}{54}=\dfrac{1}{3}\)

Do đó:

\(\left\{{}\begin{matrix}AD=\dfrac{1}{3}\cdot24=8\left(cm\right)\\CD=\dfrac{1}{3}\cdot30=10\left(cm\right)\end{matrix}\right.\)

Vậy: AD=8cm; CD=10cm

b) Xét ΔHAC vuông tại A và ΔHEB vuông tại E có 

\(\widehat{AHC}=\widehat{EHB}\)(hai góc đối đỉnh)

Do đó: ΔHAC\(\sim\)ΔHEB(g-g)

c) Xét ΔAFB vuông tại A và ΔAHC vuông tại A có 

\(\widehat{ABF}=\widehat{ACH}\left(=90^0-\widehat{AFB}\right)\)

Do đó: ΔAFB\(\sim\)ΔAHC(g-g)

Suy ra: \(\dfrac{AF}{AH}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(AF\cdot AC=AB\cdot AH=AB\cdot\dfrac{1}{3}AB=\dfrac{1}{3}AB^2\)(đpcm)

a: Xét ΔBAC vuông tại A có AH là đường cao

nên BA^2=BH*BC

b: BC=căn 18^2+24^2=30cm

CD là phân giác

=>DA/AC=DB/BC

=>DA/4=DB/5=(DA+DB)/(4+5)=18/9=2

=>DA=8cm

C

C

C

BH/HC=4/9

=>BH/BC=4/13

=>BH/4=BC/13=k

=>BH=4k; BC=13k

AB^2=BH*BC

=>52k^2=18^2

=>k^2=81/13

=>k=9/căn 13

=>BH=36/căn 13; BC=9*căn 13