cho mcầu (S) : \(^{\left(x-3\right)^2}\)+ \(\left(y-1\right)^2\)+ \(\left(z-1\right)^2\)=9. Điểm A(0;-3;-2). tìm điểm M nằm trên (S) sao cho MA Max và MB Min
Bài này bạn không nên dùng phương pháp giải tích, dùng hình học cho dễ!
Đường thẳng AO cắt mặt cầu (S) tại 2 điểm M1 và M2
Xét một đường tròn (C)= (O;R=3) bất kỳ thuộc (S) và điểm M di động trên (C) và không trùng M1, M2
Không mất tính tổng quát, điểm M có thể đại diện cho mọi điểm trên (S) (trừ M1, M2)
+) Dễ thấy \(\widehat{M_2MM_1}=90^0\),
tia M'M1 nằm giữa tia M'A và M'M2 nên \(\widehat{M_2MA}>\widehat{M_2MM_1}=90^0\)
\(\Rightarrow\widehat{M_2MA}\) là góc tù
\(\Rightarrow\Delta M_2MA\)luôn có cạnh \(AM_2>AM\)
Vậy MA max khi và chỉ khi \(M\equiv M_2\)
tìm điểm M2 bằng cách \(\frac{\overrightarrow{AM_2}}{\overrightarrow{AO}}=\frac{AM_2}{AO}=\frac{8}{5}\Rightarrow M_2\left(\frac{24}{5};\frac{17}{5};\frac{14}{5}\right)\)
+) Dễ thấy \(\widehat{AM_1M}\) là góc tù nên \(\Delta AM_1M\) luôn có \(AM>AM_1\)
Vậy MA min khi và chỉ khi \(M\equiv M_1\)
.......(làm tương tự ý trên để tìm M1 :3 )
Đúng 0
Bình luận (1)
Cho mình hỏi sao đề bài không cho tọa độ điểm B hoặc điểm B nằm ở đâu à ![]() mình cảm thấy hơi vô lý
mình cảm thấy hơi vô lý ![]()
Đúng 0
Bình luận (1)
Cho ba điểm A, B, C. Chứng minh \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)
Ta có: \(3\left( {\overrightarrow {AB} + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB} + 3\overrightarrow {BC} } \right)\)\( = 3\overrightarrow {AB} + 3.\left( {2\overrightarrow {BC} } \right) - \left[ {2\overrightarrow {AB} + 2.\left( {3\overrightarrow {BC} } \right)} \right]\)
\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - \left( {2\overrightarrow {AB} + 6.\overrightarrow {BC} } \right)\]\[ = 3\overrightarrow {AB} + 6.\overrightarrow {BC} - 2\overrightarrow {AB} - 6.\overrightarrow {BC} \]
\[ = \left( {3\overrightarrow {AB} - 2\overrightarrow {AB} } \right) + \left( {6.\overrightarrow {BC} - 6.\overrightarrow {BC} } \right) = \overrightarrow {AB} .\]
Đúng 0
Bình luận (0)
Cho hàm số y {x^2} + 2x - 3.a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b) Vẽ các điểm Aleft( { - 3;0} right),Bleft( { - 2; - 3} right),Cleft( { - 1; - 4} right),Dleft( {0; - 3} right),Eleft( {1;0} right) của đồ thị hàm số y {x^2} + 2x - 3 trong mặt phẳng tọa độ Oxy.c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số y {x^2} + 2x - 3 (Hình 11).d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol...
Đọc tiếp
Cho hàm số \(y = {x^2} + 2x - 3\).
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy.
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11).
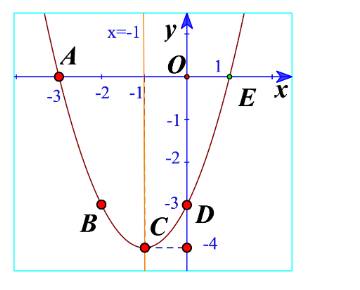
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm \(A\left(1;2\right);B\left(-2;4\right);C\left(2;m\right)\). Hãy tìm m để 3 điểm A, B, C thẳng hàng ?
\(\overrightarrow{AB}\left(-3;2\right)\); \(\overrightarrow{AC}\left(1;m-2\right)\).
Ba điểm A, B, C thẳng hàng khi và chỉ khi:
\(\dfrac{1}{-3}=\dfrac{m-2}{2}\Leftrightarrow-3\left(m-2\right)=2\)\(\Leftrightarrow m=\dfrac{4}{3}\).
Đúng 0
Bình luận (0)
1.Cho hình vuông ABCD cạnh a . Tính left|overrightarrow{AD}+overrightarrow{3AB}right| theo a 2. Cho tam giác ABC đều cạnh a. M là trung điểm BC . Tính left|overrightarrow{MA}+3overrightarrow{MB}+overrightarrow{MC}right|theo a 3. Cho tam giác ABC đều cạnh a có G là trọng tâm . Tính left|overrightarrow{AB}-overrightarrow{GC}right|theo aGiups mik vs ạ . Tks
Đọc tiếp
1.Cho hình vuông ABCD cạnh a . Tính \(\left|\overrightarrow{AD}+\overrightarrow{3AB}\right|\) theo a
2. Cho tam giác ABC đều cạnh a. M là trung điểm BC . Tính \(\left|\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC}\right|\)theo a
3. Cho tam giác ABC đều cạnh a có G là trọng tâm . Tính \(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|\)theo a
Giups mik vs ạ . Tks
1.
Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)
\(=AD^2+9AB^2=10AB^2=10a^2\)
\(\Rightarrow P=a\sqrt{10}\)
2.
Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)
\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)
\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)
\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)
\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)
Đúng 2
Bình luận (0)
Cho bốn điểm \(A\left( {7; - 3} \right),B\left( {8;4} \right),C\left( {1;5} \right),D\left( {0; - 2} \right)\). Chứng minh rằng tứ giác ABCD là hình vuông.
Ta có: \(\overrightarrow {AB} = (1;7),\overrightarrow {AD} = ( - 7;1),\overrightarrow {CD} = ( - 1; - 7)\),\(\overrightarrow {BC} = ( - 7;1)\)
Suy ra \(AB = \overrightarrow {AB} = \sqrt {{1^2} + {7^2}} = 5\sqrt 2 ,AD = \overrightarrow {AD} = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} = 5\sqrt 2 ,\)
\(CD = \overrightarrow {CD} = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 7} \right)}^2}} = 5\sqrt 2 \),\(BC = \overrightarrow {BC} = \sqrt {{{\left( { - 7} \right)}^2} + {{\left( { - 1} \right)}^2}} = 5\sqrt 2 \)
\( \Rightarrow AB = BC = CD = DA = 5\sqrt 2 \) (1)
Mặt khác ta có
\(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AD} }}{{AB.AD}} = \frac{{1.( - 7) + 7.1}}{{5\sqrt 2 .5\sqrt 2 }} = 0 \Rightarrow \widehat A = 90^\circ \) (2)
Từ (1) và(2) suy ra ABCD là hình vuông (đpcm)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu left(Sright):left(x+1right)^2+left(y-2right)^2+left(z-3right)^248 và đường thẳng left(dright):dfrac{x+1}{1}dfrac{y-2}{1}dfrac{z-3}{sqrt{2}} . Điểm Mleft(a;b;cright)left(a0right) nằm trên đường thẳng left(dright) sao cho từ M kẻ được 3 tiếp tuyến MA,MB,MC đến mặt cầu left(Sright) thỏa mãn widehat{AMB}60^o,widehat{BMC}90^o,widehat{CMA}120^o. Tính Qa+b-c?
Đọc tiếp
Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left(S\right):\left(x+1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=48\) và đường thẳng \(\left(d\right):\dfrac{x+1}{1}=\dfrac{y-2}{1}=\dfrac{z-3}{\sqrt{2}}\) . Điểm \(M\left(a;b;c\right)\left(a>0\right)\) nằm trên đường thẳng \(\left(d\right)\) sao cho từ \(M\) kẻ được 3 tiếp tuyến \(MA,MB,MC\) đến mặt cầu \(\left(S\right)\) thỏa mãn \(\widehat{AMB}=60^o,\widehat{BMC}=90^o,\widehat{CMA}=120^o\). Tính \(Q=a+b-c\)?
Cho hàm số \(Y=F\left(x\right)=\frac{1}{2}x^2-1\)
A) \(F\left(\frac{-1}{2}\right),F\left(0\right),F\left(-2\right),F\left(\frac{3}{4}\right)\)
B)Cho điểm \(A\left(4;7\right)\)\(B\left(-1;\frac{1}{2}\right)\).Hỏi điểm nào thuộc đồ thị của hàm số ? Vì sao ?
Cho ba điểm \(B=\left(-2;3\right)\) ;\(C=\left(3;3\right)\) ;\(D=\left(3;-2\right)\) . Biết A là điểm có tọa độ sao cho 4 điểm A; B; C; D tạo thành hình vuông. Tính diện tích hình vuông ABCD.
Theo hệ trục toạ độ ( bạn tự vẽ nha ), để ABCD là hình vuông => \(A\left(-2;-2\right)\)
Ta có : độ dài AB=\(\sqrt{\left(-2+2\right)^2+\left(-2-3\right)^2}=\sqrt{25}=5\)
=> Diện tích của hình v ABCD=\(5^2=25\)( đơn vị )
Đúng 0
Bình luận (0)
cho tam giác ABC ;M;N là 2 điểm sao cho overrightarrow{AM}frac{1}{2}overrightarrow{AB}VÀ overrightarrow{AN}frac{2}{3}overrightarrow{AC} VÀ K là trung điểm của MN.A) Biểu diễn AK theo AB;AC b) với A( 1;0) ;B(-3;-5) ;C(0;3) .+, tìm M;N;K+ Xd điểm E sao cho AECE5+ tìm tập hợp điểm P sao cho left|2left(overrightarrow{PA}+overrightarrow{PB}right)-3overrightarrow{PC}right|left|overrightarrow{PB}-overrightarrow{PC}right|
Đọc tiếp
cho tam giác ABC ;M;N là 2 điểm sao cho \(\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}\)VÀ \(\overrightarrow{AN}=\frac{2}{3}\overrightarrow{AC}\) VÀ K là trung điểm của MN.
A) Biểu diễn AK theo AB;AC
b) với A( 1;0) ;B(-3;-5) ;C(0;3) .
+, tìm M;N;K
+ Xd điểm E sao cho AE=CE=5
+ tìm tập hợp điểm P sao cho \(\left|2\left(\overrightarrow{PA}+\overrightarrow{PB}\right)-3\overrightarrow{PC}\right|=\left|\overrightarrow{PB}-\overrightarrow{PC}\right|\)

