Ta co 2 đường tròn (A ; 3cm) và (B : 2cm) cắt nhau tại C, D.
AB = 4cm. Đường tròn tâm A, B lần lượt cắt đoạn thẳng AB tại K, I.
a) Tính CA, CB, DA, DB.
b) I có phải là trung điểm của đoạn thẳng AB không? (mình ko vẽ được hình nhưng I là trung điểm của đoạn thẳng AB)
c) Tính IK
Mình đang cần gấp!!
Ai trả lời nhanh và đúng nhất mình sẽ tick!!
Các bạn ko cần phải vẽ hình.


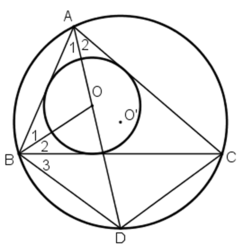

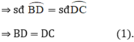
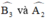 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 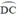
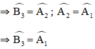
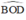 là góc ngoài của tam giác
là góc ngoài của tam giác
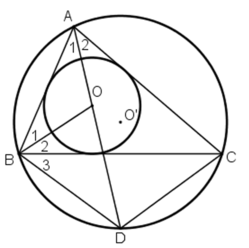

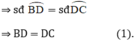
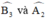 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 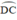
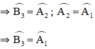
 là góc ngoài của tam giác
là góc ngoài của tam giác