Giải hộ mình bài này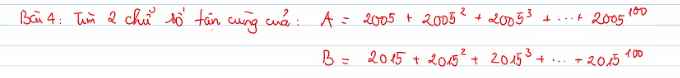 ❕
❕
NH
Những câu hỏi liên quan
Giúp mình bài này với❕
 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !
Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Đúng 2
Bình luận (0)
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm
Đúng 2
Bình luận (0)
các bn tốt bụng giúp mk pài này nx nhá: tìm các cặp số nguyên x,y thỏa mãn xy-2x+y+1=0. giúp nhanh và giải chi tiết hộ mk với nhé❕.
thank you c.bn nhìuuuuu
\(xy-2x+y+1=0\\ x\left(y-2\right)+\left(y-2\right)=-3\\ \left(x+1\right)\left(y-2\right)=-3\)
Lập bảng
| x+1 | 1 | 3 | -1 | -3 |
| y-2 | 3 | 1 | -3 | -1 |
| x | 0 | 2 | -2 | -4 |
| y | 5 | 3 | -1 | 1 |
Vậy \(\left(x;y\right)\in\left\{\left(0;5\right);\left(2;3\right);\left(-2;-1\right);\left(-4;1\right)\right\}\)
Đúng 0
Bình luận (0)
xy−2x+y+1=0x(y−2)+(y−2)=−3(x+1)(y−2)=−3xy−2x+y+1=0x(y−2)+(y−2)=−3(x+1)(y−2)=−3
Lập bảng
| x+1 | 1 | 3 | -1 | -3 |
| y-2 | 3 | 1 | -3 | -1 |
| x | 0 | 2 | -2 | -4 |
| y | 5 | 3 | -1 | 1 |
Vậy (x;y)∈{(0;5);(2;3);(−2;−1);(−4;1)}
Đúng 0
Bình luận (0)
Giải hộ mình bài này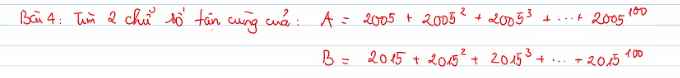
Các bạn giải hộ mình bài này nhé giải chia tiết giúp mình
e: \(=\dfrac{-3}{4}+\dfrac{5}{7}=\dfrac{-21+20}{28}=\dfrac{-1}{28}\)
Đúng 1
Bình luận (0)
a ) \(\dfrac{6}{13}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{6.3}{13.3}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{18}{39}\) - \(\dfrac{14}{39}\)
= \(\dfrac{4}{39}\)
{ các ý còn lại tương tự }
Đúng 1
Bình luận (1)
các bạn ơi giải hộ mình bài này, mình chỉ cần bài 6 thôi

Giải hộ mình bài này với .....

| Vượn cổ | Người tối cổ | Người tinh khôn | |
| Thời gian xuất hiện | khoảng 6 triệu năm trước | 4 triệu nằm trước đây | khoảng 4 vạn nằm trước đây |
Cấu tạo cơ thể
| - Có thể đi, đứng bằng 2 chân | - Đi, đứng bằng hai chân. - Trán thấp và bợt ra sau, u mày nổi cao, hộp sọ đã lớn hơn và hình thành trung tâm phát tiếng nói trong não. | - Như con người ngày nay |
| Địa điểm xuất hiện | ở Đông Phi,Tây Á, Việt Nam | ở Đông Phi, Gia va, Bắc kinh, Thanh Hóa | ở hầu hết các châu lục |
Đúng 1
Bình luận (0)
giải hộ mình bài này cái 
1. Jim asked his girlfriend how many pairs of shoes does she have.
2. Peter asked Jane if she is going to London next week.
3. Mom asked my sister if she had done the laundry.
4. Jane asked Peter if his brother lived in London.
5. Jim asked his sister what was she doing now.
6. My classmate asked me if I enjoyed the party last night.
7. My friends always ask me what genre of music do I most.
8. My doctor asked me what had I done to cope with my work stress.
9. Jim asked me what did I often do if I was sad.
10. Jim asked me who did I run into yesterday.
Giải hộ mình bài này với.
Giải hộ mình bài này với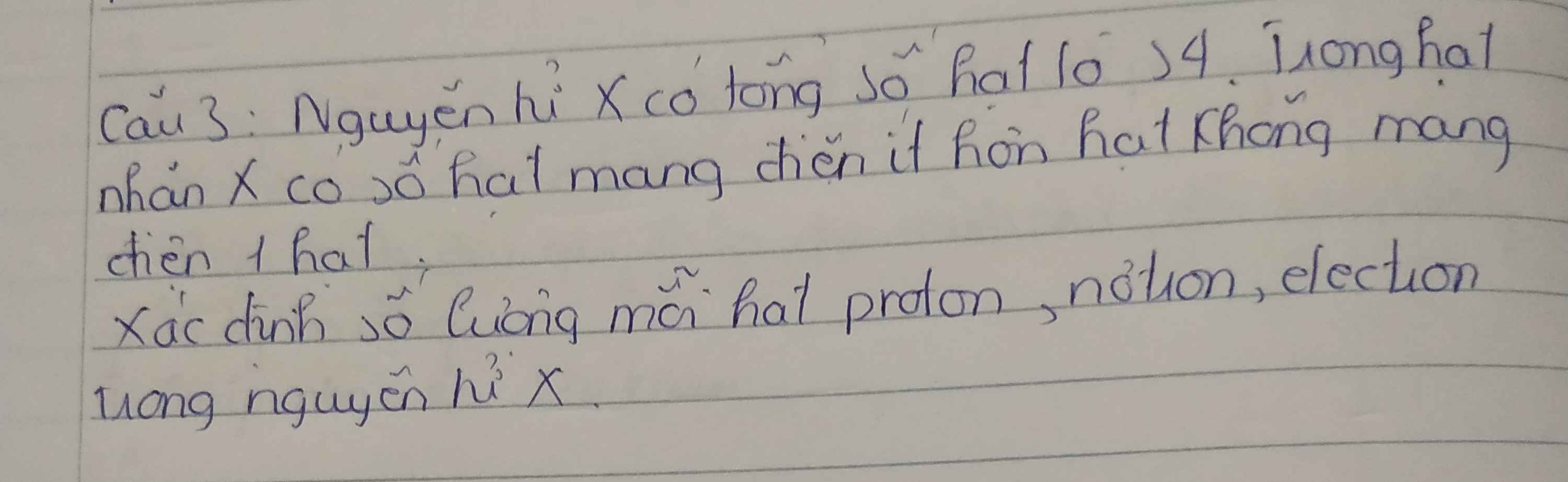
\(Tacó:\left\{{}\begin{matrix}2Z+N=34\\N-Z=1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}Z=11=P=E\\N=12\end{matrix}\right.\)
Đúng 0
Bình luận (0)





