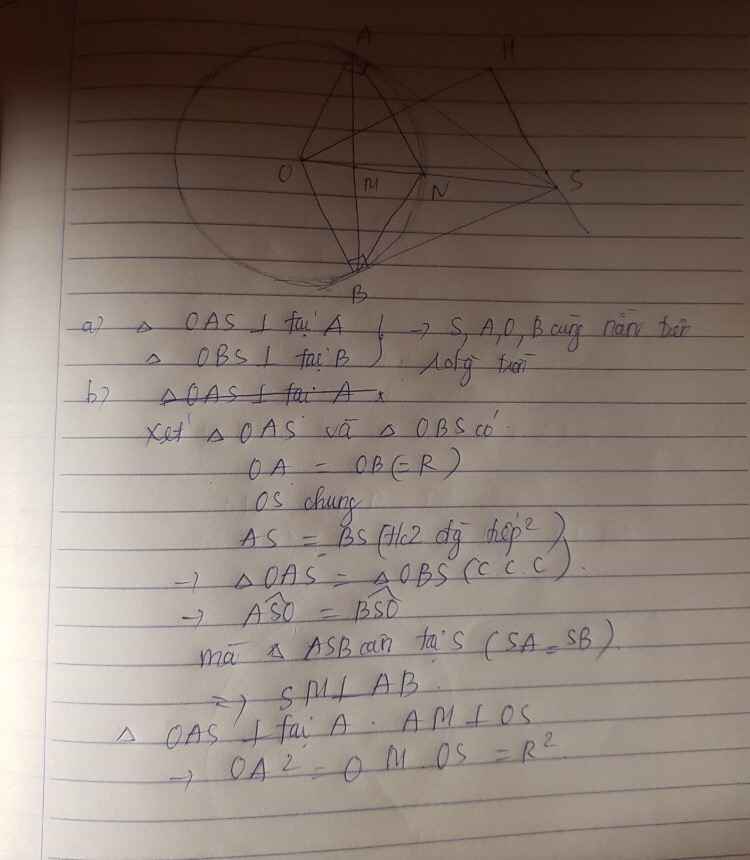Giúp em với
Em chưa học tứ giác nội tiếp ạ
VP
Những câu hỏi liên quan
Giúp em với !!!!!!!
Em chưa học tứ giác nội tiếp ạ
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Giúp em với
Em chưa học tứ giác nội tiếp ạ
Bài 2,3 ạ..EM CẦN GẤPPPPP,KHÔG DÙNG TỨ GIÁC NỘI TIÉP Ạ VÌ EM CHƯA HỌC Ạ
Giúp em bài này cs ko dùng đường tròn nội tiếp ạ vì em chưa học 
a)Xét ΔABC cân tại A có AE là trung tuyến
⇒ AE cũng là đường cao của ΔABC
⇒ AE⊥BC \(\Rightarrow\widehat{AEB}=\widehat{AEC}=90^o\)
Xét tứ giác ADBE có \(\widehat{ADB}\) và \(\widehat{AEB}\) cùng nhìn AB dưới góc 90o
⇒ ADBE là tứ giác nội tiếp
⇒ 4 điểm A,D,B,E cùng thuộc (O)
b) Vì BD⊥AC hay HD⊥AC ⇒ ΔHDC vuông tại D
⇒ Tâm của đường tròn đi qua 3 điểm H,D,C là trung điểm của HC
hay I là trung điểm của HC
c) Xét tứ giác HDCE có 2 góc đối \(\widehat{HDC}+\widehat{HEC}=90^o+90^o=180^o\)
⇒ HDCE là tứ giác nội tiếp
⇒ 2 điểm H,E thuộc (I)
Mà 2 điểm H,E cũng thuộc (O)
⇒ Đường tròn tâm O và đường tròn tâm I có 2 điểm chung
Đúng 0
Bình luận (0)
a: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến ứng với cạnh đáy BC
nên AE là đường cao ứng với cạnh BC
Xét tứ giác ADEB có
\(\widehat{ADB}=\widehat{AEB}=90^0\)
Do đó: ADEB là tứ giác nội tiếp
hay A,D,E,B cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
b: Ta có: ΔHDC vuông tại D
nên ΔHDC nội tiếp đường tròn đường kính HC
hay I là trung điểm của HC
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O).3 đường cao AD,BE,CF cắt nhau ở H.(AB<AC).Chứng minh:
a,BCEF,AEHF là tứ giác nội tiếp.
b,2 đường thẳng BC,EF cắt nhau ở M.MA cắt đường tròn(O) ở I.Chứng minh AIFE là tứ giác nội tiếp.
c,Chứng minh :Góc AIH = 90 độ.
Em đang cần gấp ạ!Mọi người giúp em với ạ!Em cảm ơn mọi người trước ạ!
anh chị giúp em bài này với ạ chứng minh nếu 1 tứ giác nội tiếp 1 đường tròn thì tích 2 đường chéo bằng tổng các tích 2 cạnh đối diện
giúp em với ạ :(((
cho tam giác abc (ab<ac ) nội tiếp đường tròn tâm o , đường cao ah , ah cắt đường tròn ở d , ao cắt đường tròn ở e. chứng minh góc bah = góc oac , tứ giác bced là hình gì ?
a, ABDC nội tiếp
=> ˆBAH = ˆBCD
ACED nội tiếp
=> OAC^ = CDE^
Lại có ΔDEA nội tiếp đường tròn đường kínhAE
=> DE ⊥ AD
mà AD ⊥ BC
=> DE // BC=>BCD^ =CDE^ ( so le trong)
=>BAH^ = OAC^
b, DE // BC=> BDEC là hình thang (*)
Lại có:
DBC^ = DAC^ ( BDAC nội tiếp) (1)
BCE^= EAB^ ( ABEC nội tiếp) (2)
Lại có: BAH^ = OAC^
=> BAH^ + HAO^ = OAC^ + ˆHAO
=> EAB^ = DAC^ (3)
Từ (1) (2) (3) => DBC^= BCE^ (**)
từ (*) và (**) => BCED là hình thang cân
Đúng 0
Bình luận (0)
Các bác giúp em bài này với ạ. Em cảm ơn!
Chứng minh rằng các đa giác đều là đa giác nội tiếp.
Các thầy cô, các bạn giúp em với!!! Em cảm ơn trước!Cho tam giác vuông ABC (BC AB, góc B90 độ). Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm của đường tròn nội tiếp với cạnh AB, BC, CA lần lượt là P, Q, R.1) Chứng minh tứ giác BPIQ là hình vuông. (bỏ qua )2) Đường thẳng BI cắt QR tại D. Chứng minh 5 điểm P, A, R, D, I nằm trên một đường tròn.3) Đường thẳng AI và CI kéo dài cắt BC, AB lần lượt tại E và F. Chứng minh AE. CF 2AI. CI.
Đọc tiếp
Các thầy cô, các bạn giúp em với!!! Em cảm ơn trước!
Cho tam giác vuông ABC (BC > AB, góc B=90 độ). Gọi I là tâm đường tròn nội tiếp tam giác ABC, các tiếp điểm của đường tròn nội tiếp với cạnh AB, BC, CA lần lượt là P, Q, R.
1) Chứng minh tứ giác BPIQ là hình vuông. (bỏ qua )
2) Đường thẳng BI cắt QR tại D. Chứng minh 5 điểm P, A, R, D, I nằm trên một đường tròn.
3) Đường thẳng AI và CI kéo dài cắt BC, AB lần lượt tại E và F. Chứng minh AE. CF = 2AI. CI.