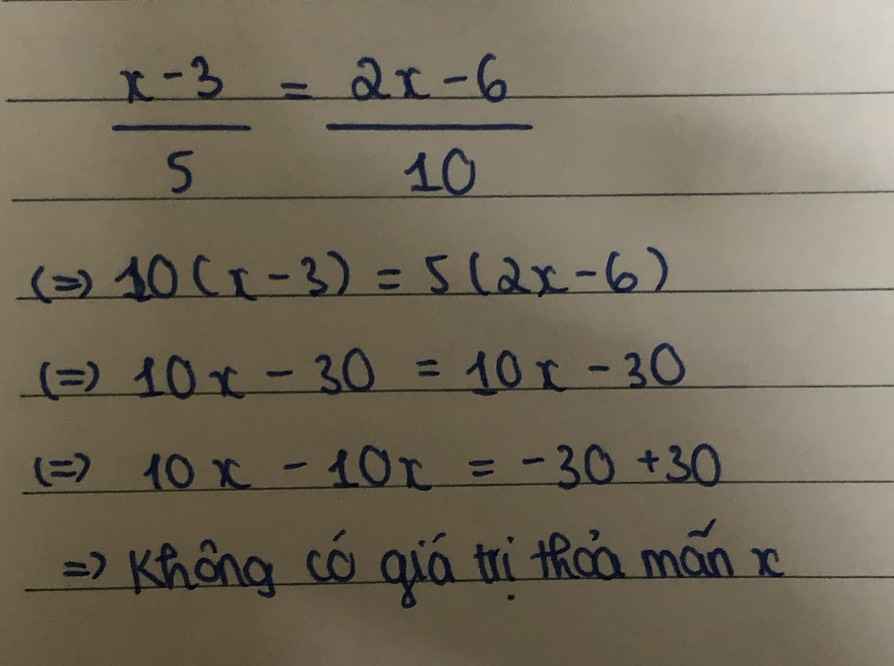\(0.25x-\dfrac{3}{4}x=-\dfrac{2}{5}\)
giúp mình với mình đang ôn thi ![]()
ND
Những câu hỏi liên quan
\(\dfrac{x-3}{5}\)=\(\dfrac{2x-6}{10}\)
Em đang ôn thi, giúp em với ạ! Em cảm ơn.
`[x-3]/5=[2x-6]/10`
`[2(x-3)]/10=[2x-6]/10`
`2x-6=2x-6`
`2x-2x=-6+6`
`0x=0` (LĐ)
Vậy `x in RR`
Đúng 2
Bình luận (2)
a, x =\(\dfrac{-2}{7}\) +\(\dfrac{9}{7}\)
b,\(\dfrac{x}{3}\) =\(\dfrac{2}{5}\) +\(\dfrac{-4}{3}\)
Làm giúp mik vs mình đang cần gấp!
a) \(x=\dfrac{-2}{7}+\dfrac{9}{7}=1\)
b) \(\dfrac{x}{3}=\dfrac{2}{5}+\dfrac{-4}{3}\)
\(\dfrac{x}{3}=\dfrac{-14}{15}\)
\(\Rightarrow x=\dfrac{3.-14}{15}=\dfrac{-14}{5}\)
Đúng 1
Bình luận (0)
\(x=\dfrac{-2}{7}+\dfrac{9}{7}\)
\(x=1\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP:
a, Tính \(\int\left(\dfrac{1}{4}\right)\)và \(\int\left(-1\right)\)
b, Tìm x để \(\int\)(x) = -3
c, ( x - \(\dfrac{2}{5}\))\(^2\) = \(\dfrac{1}{4}\)
c: \(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{2}{5}=\dfrac{1}{2}\\x-\dfrac{2}{5}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{10}\\x=-\dfrac{1}{10}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải hệ phương trình:
\(\left\{{}\begin{matrix}2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)=\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\\16x^5-20x^3+5\sqrt{xy}=\sqrt{\dfrac{y+1}{2}}\end{matrix}\right.\)
Mình đang cần gấp lắm, các bạn giúp mình với. Cảm ơn!
\(\left\{{}\begin{matrix}2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)=\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\left(1\right)\\16x^5-20x^3+5\sqrt{xy}=\sqrt{\dfrac{y+1}{2}}\left(2\right)\end{matrix}\right.\).
ĐKXĐ: \(xy>0;y\ge-\dfrac{1}{2}\).
Nhận thấy nếu x < 0 thì y < 0. Suy ra VT của (1) âm, còn VP của (1) dương (vô lí)
Do đó x > 0 nên y > 0.
Với a, b > 0 ta có bất đẳng thức \(\left(a+b\right)^4\le8\left(a^4+b^4\right)\).
Thật vậy, áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(\left(a+b\right)^4\le\left[2\left(a^2+b^2\right)\right]^2=4\left(a^2+b^2\right)^2\le8\left(a^4+b^4\right)\).
Dấu "=" xảy ra khi và chỉ khi a = b.
Áp dụng bất đẳng thức trên ta có:
\(\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^4\le8\left[8\left(x^4+y^4\right)+16x^2y^2\right]=64\left(x^2+y^2\right)^2\)
\(\Rightarrow\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\le8\left(x^2+y^2\right)\). (3)
Lại có \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2=4\left(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\right)\). (4)
Áp dụng bất đẳng thức AM - GM ta có \(\dfrac{x^6}{y^4}+xy+xy+xy+xy\ge5x^2;\dfrac{y^6}{x^4}+xy+xy+xy+xy\ge5y^2;3\left(x^2+y^2\right)\ge6xy\).
Cộng vế với vế của các bđt trên lại rồi tút gọn ta được \(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\ge2\left(x^2+y^2\right)\). (5)
Từ (3), (4), (5) suy ra \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2\ge\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\Rightarrow2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)\ge\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\).
Do đó đẳng thức ở (1) xảy ra nên ta phải có x = y.
Thay x = y vào (2) ta được:
\(16x^5-20x^3+5x=\sqrt{\dfrac{x+1}{2}}\). (ĐK: \(x>0\))
PT này có một nghiệm là x = 1 mà sau đó không biết giải ntn :v
Đúng 0
Bình luận (0)
Giúp mình với, mình đang cần gấp
\(\dfrac{x^3}{1-x}\) + x2 + x + 1
\(\dfrac{2x}{x^2+4x+4}\) + \(\dfrac{x+1}{x+2}\) + \(\dfrac{2-x}{\left(x+2\right)^2}\)
Xin cảm ơn <3
\(a,=\dfrac{x^3-\left(x-1\right)\left(x^2+x+1\right)}{1-x}=\dfrac{x^3-x^3+1}{1-x}=\dfrac{1}{1-x}\\ b,=\dfrac{2x+x^2+3x+2+2-x}{\left(x+2\right)^2}=\dfrac{\left(x+2\right)^2}{\left(x+2\right)^2}=1\)
Đúng 1
Bình luận (1)
tìm x biết
\(\dfrac{7}{9}:\left(2+\dfrac{3}{4}.x\right)+\dfrac{5}{9}=\dfrac{23}{27}\)
|x|\(-\dfrac{3}{4}=\dfrac{5}{3}\)
\(\left|2.x-\dfrac{1}{3}\right|+\dfrac{5}{6}=1\)
giúp mk vs nhanh lên mình đang bận
b) Ta có: \(\left|x\right|-\dfrac{3}{4}=\dfrac{5}{3}\)
\(\Leftrightarrow\left|x\right|=\dfrac{5}{3}+\dfrac{3}{4}=\dfrac{20}{12}+\dfrac{9}{12}=\dfrac{29}{12}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{29}{12}\\x=-\dfrac{29}{12}\end{matrix}\right.\)
c) Ta có: \(\left|2x-\dfrac{1}{3}\right|+\dfrac{5}{6}=1\)
\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{1}{3}=\dfrac{1}{6}\\2x-\dfrac{1}{3}=\dfrac{-1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{6}+\dfrac{1}{3}=\dfrac{1}{2}\\2x=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=\dfrac{1}{12}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 2.4 Chứng minh với mọi giá trị của x để biểu thức có nghĩa thì giá trị của:
𝐴= \((\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}+\dfrac{3}{x-1}-\dfrac{\sqrt{x+3}}{2\sqrt{x}+2}).\dfrac{4x-4}{5}\) không phụ thuộc vào x.
ai bt giúp mình với mình đang cần gấp
A = \(\left(\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}+\dfrac{3}{x-1}-\dfrac{\sqrt{x}+3}{2\sqrt{x}+2}\right)\cdot\dfrac{4x-4}{5}\) (ĐK: x \(\ge\) 0; x \(\ne\) 1)
A = \(\left(\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}+\dfrac{3}{x-1}-\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{4\left(x-1\right)}{5}\)
A = \(\left(\dfrac{\left(\sqrt{x}+1\right)^2}{2\left(x-1\right)}+\dfrac{6}{2\left(x-1\right)}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{2\left(x-1\right)}\right)\cdot\dfrac{4\left(x-1\right)}{5}\)
A = \(\left(\dfrac{x+2\sqrt{x}+1+6-x-3\sqrt{x}+\sqrt{x}+3}{2\left(x-1\right)}\right)\cdot\dfrac{4\left(x-1\right)}{5}\)
A = \(\dfrac{10}{2\left(x-1\right)}\cdot\dfrac{4\left(x-1\right)}{5}\)
A = 4
Vậy A không phụ thuộc vào x
Chúc bn học tốt!
Đúng 1
Bình luận (0)
Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}+\dfrac{3}{x-1}-\dfrac{\sqrt{x}+3}{2\sqrt{x}+2}\right)\cdot\dfrac{4x-4}{5}\)
\(=\dfrac{x+2\sqrt{x}+1+6-\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{4\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{5}\)
\(=\dfrac{x+2\sqrt{x}+7-x-2\sqrt{x}+3}{1}\cdot\dfrac{2}{5}\)
\(=10\cdot\dfrac{2}{5}=4\)
Đúng 1
Bình luận (0)
Tính bằng cách thuận tiện nhất
a, \(\dfrac{1}{10}+\dfrac{2}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{5}{10}+\dfrac{6}{10}+\dfrac{7}{10}+\dfrac{8}{10}+\dfrac{9}{10}\)
b, 13,25 : 0,5 + 13,25 : 0,25 + 13,25 : 0,125 + 13,25 x 6
Giúp mình với mình đang gấp
\(\dfrac{1}{10}+\dfrac{2}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{5}{10}+\dfrac{6}{10}+\dfrac{7}{10}+\dfrac{8}{10}+\dfrac{9}{10}\)
\(=\left(\dfrac{1}{10}+\dfrac{9}{10}\right)+\left(\dfrac{2}{10}+\dfrac{8}{10}\right)+\left(\dfrac{3}{10}+\dfrac{7}{10}\right)+\left(\dfrac{4}{10}+\dfrac{6}{10}\right)+\dfrac{5}{10}\)
\(=1+1+1+1+\dfrac{5}{10}\)
\(=4+\dfrac{5}{10}\)
\(=\dfrac{45}{10}\)
\(13,25:0,5+13,25:0,25+13,25:0,125+13,25\times6\)
\(=13,25:\dfrac{1}{2}+13,25:\dfrac{1}{4}+13,25:\dfrac{1}{8}+13,25\times6\)
\(=13,25\times2+13,25\times4+13,25\times8+13,25\times6\)
\(=13,25\times\left(2+4+8+6\right)\)
\(=13,25\times20\)
\(=265\)
Đúng 0
Bình luận (0)
Tìm các số tự nhiên x,y biết: \(\dfrac{1}{x}\) + \(\dfrac{y}{3}\) = \(\dfrac{5}{6}\)
Giúp mình với mình đang cần gấp!!!
=> 1/x = 5/6 - y/3
1/x = 5-2y/6
=> x(5-2y) = 1.6 = 6
Do x ∈ N => x >= 0
Mà 6>0 => 5-2y > 0
Vì y ∈ N => 5-2y ∈ N*
Ta có bảng:
| x | 1 | 3 | 6 |
| 5-2y | 6 | 2 | 1 |
| y | -0,5 | 2,5 | 2 |
Do x,y ∈ N => (x,y) = (6,2) (thử lại thỏa mãn)
Vậy x=6; y = 2
Đúng 2
Bình luận (0)