

Mng giúp mik với ạ
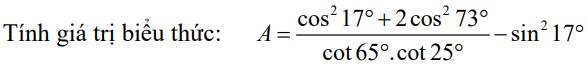
Mng giúp mik với ạ. Mik cảm ơn.
\(A=\dfrac{\cos^217^o+2\cos^273^o}{\cot65^o\cot25^o}-\sin^217^o\)
\(A=\dfrac{\left(\cos^217^o+\cos^273^o\right)+\cos^273^o}{\tan25^o\cot25^o}-\sin^217^o\)
(áp dụng công thức \(\cot\alpha=\tan\left(90^o-\alpha\right)\))
\(A=\left(\cos^217^o+\sin^217^o\right)+\sin^217^o-\sin^217^o\)
(áp dụng công thức \(\tan\alpha.\cot\alpha=1\) và \(\cos\alpha=\sin\left(90^o-\alpha\right)\))
\(A=1\)
Mng giúp mik với ạ
Giúp mik với mng ơi , mik đang cần gấp ạ
giúp mik với ạ, mik đang cần gấp! cảm ơn mng nhìu!
\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
mng ơi lm chi tiết giúp mik với ạ
Bài 2:
a: \(\dfrac{-5}{9}+\dfrac{4}{9}=\dfrac{-1}{9}\)
b: \(=\dfrac{5}{17}+\dfrac{-1}{17}\cdot3=\dfrac{5}{17}-\dfrac{3}{17}=\dfrac{2}{17}\)
c: \(=\dfrac{1}{5}\left(\dfrac{4}{7}+\dfrac{3}{7}\right)-\dfrac{1}{5}=\dfrac{1}{5}-\dfrac{1}{5}=0\)
d: =5,17-2,24-5,17+3,24=1
giúp mik bài này với ạ. Cảm ơn mng huhu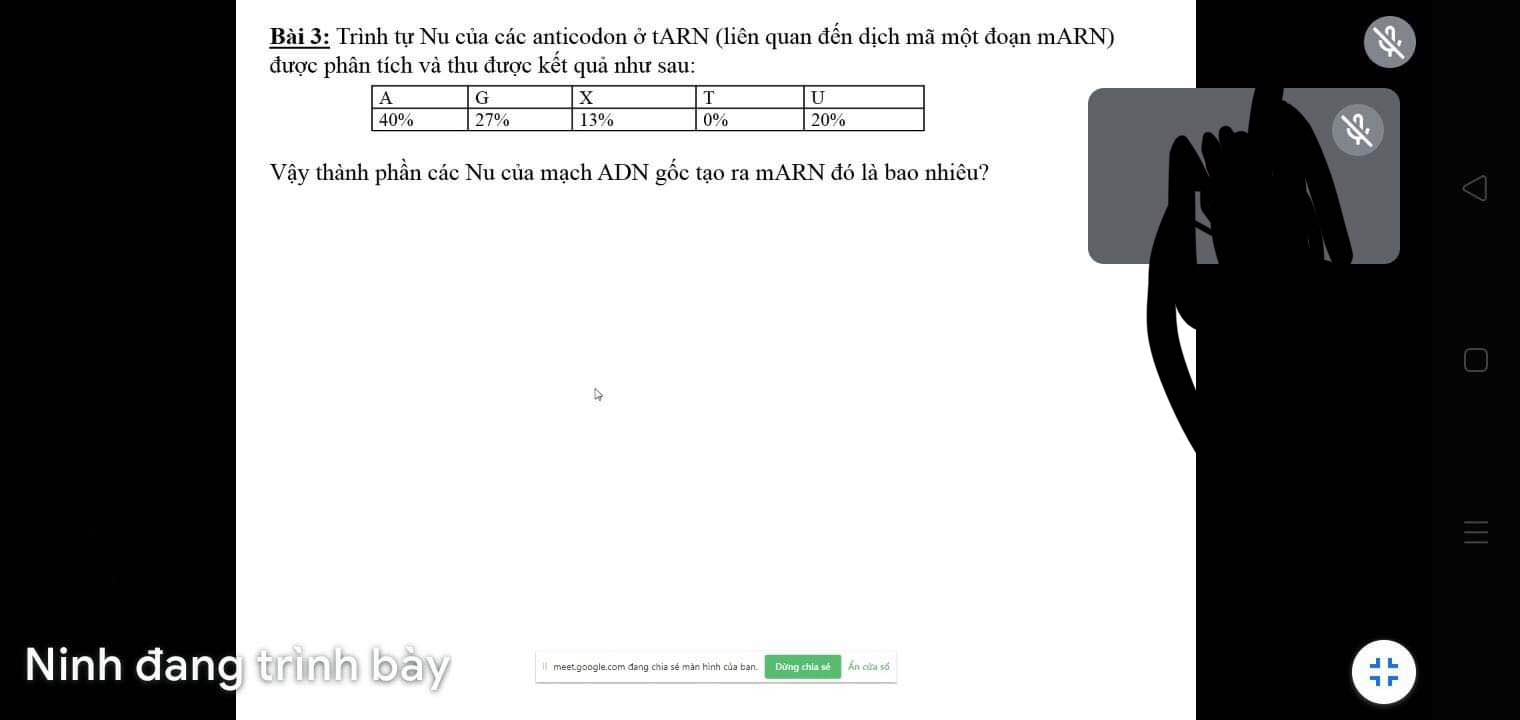
Trên ADN:
A = 40%, T = 20%, G = 27%, X = 13%
Trên ADN:
Amạch gốc =mU = 40%
Tmạch gốc =mA = 20%
Gmạch gốc = mX = 27%
Xmạch gốc =mG= 13%
mng giải giúp mik vs ạ, vẽ hộ cả hình với
a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM
Mng cho mik hỏi với:
-Chính sách cai trị tiêu biểu và chính sách đối ngoại của triều đại Đường là j ạ?
Mong mng trả lời giúp mik cảm ơn ạ.
Giúp mik vs ạ, mik đang cần gấp. Mong mng giúp ạ

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)
\(A=\dfrac{-4x^2+x^2-2x+1-x^2-2x-1}{\left(1-x\right)\left(1+x\right)}=\dfrac{-4x\left(x+1\right)}{\left(1-x\right)\left(1+x\right)}=\dfrac{4x}{x-1}\\ C=\dfrac{-x^2-4x-4+x^2-4x+4-4x^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{-4x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x}{2-x}\\ E=\dfrac{x^2-9-x^2+4x-4-x^2+9}{\left(x-2\right)\left(x+3\right)}=\dfrac{-\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}=\dfrac{2-x}{x+3}\)