Cho lục giác lồi ABCDEF có các cặp cạnh đối song song với nhau. Chứng minh rằng SACE >= 1/2 SABCDEF
TB
Những câu hỏi liên quan
Cho lục giác lồi abcdef có các cặp cạnh đối ab và de, bc và ef, CD và ef vừa song song vừa bằng nhau. Lục giác abcdef có nhất thiết là lục giác đều không
Cho lục giác lồi ABCDEF. Gọi \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF,FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh đối diện song song và bằng nhau.
Cho lục giác lồi ABCDEF. Gọi \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF,FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh đối diện song song và bằng nhau.
Cho lục giác lồi ABCDEF, gọi các điểm \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF, FEA, FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh song song và bằng nhau.
Cho lục giác lồi ABCDEF, gọi các điểm \(A_1,B_1,C_1,D_1,E_1,F_1\) theo thứ tự là trọng tâm tam giác ABC, BCD, CDE, DEF, FEA, FAB. Chứng minh rằng lục giác \(A_1B_1C_1D_1E_1F_1\) có các cạnh song song và bằng nhau.
Cần chứng minh
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\), \(_{ }\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\), \(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\)
Ta có :
\(\overrightarrow{OA_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\) ; \(\overrightarrow{OD_1}=\frac{\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}\)
\(\overrightarrow{OB_1}=\frac{\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}}{3}\) ; \(\overrightarrow{OE_1}=\frac{\overrightarrow{OE}+\overrightarrow{OF}+\overrightarrow{OA}}{3}\)
Từ đó suy ra :
\(\overrightarrow{A_1B_1}+\overrightarrow{OD_1}=\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}}{3}=\overrightarrow{0B_1}+\overrightarrow{OE_1}\)
và do đó
\(\overrightarrow{A_1B_1}=\overrightarrow{E_1D_1}\)
Tương tự ta cũng có \(\overrightarrow{B_1C_1}=\overrightarrow{F_1E_1}\) ,\(\overrightarrow{C_1D_1}=\overrightarrow{A_1F_1}\) => Điều phải chứng minh
Đúng 0
Bình luận (0)
cho lục giác abcdef có cặp cạnh đối song song và bằng nhau cmr các đường chéo ad,be,cf đồng qui
cho lục giác abcdef có cặp cạnh đối song song và bằng nhau cmr các đường chéo ad,be,cf đồng qui
gọi giao điểm của AD và EB là O mà ABDE là hình bình hành nên O là trung điểm EB
Nối BF ; CE ta đc BCEF là hình bình hành nên EB và CF cắt nhau tại trung điểm EB là O
Đúng 0
Bình luận (0)
LP
23 tháng 8 2023 lúc 21:16
Cho lục giác lồi A_1A_2A_3A_4A_5A_6 có diện tích bằng 1 và có các cặp cạnh đối song song, hai đường thẳng A_6A_1; A_2A_3 cắt nhau tại điểm B_1, hai đường thẳng A_1A_2;A_3A_4 cắt nhau tại điểm B_2.;...; tương tự, A_{i-1}A_i;A_{i+1}A_{i+2} cắt nhau tại điểm B_i (xem A_7 là A_1 và A_8 là A_2). Chứng minh rằng tổng diện tích của sáu tam giác A_iB_iA_{i+1}, i1,...,6 không bé hơn 1.
Đọc tiếp
Cho lục giác lồi \(A_1A_2A_3A_4A_5A_6\) có diện tích bằng 1 và có các cặp cạnh đối song song, hai đường thẳng \(A_6A_1\); \(A_2A_3\) cắt nhau tại điểm \(B_1\), hai đường thẳng \(A_1A_2;A_3A_4\) cắt nhau tại điểm \(B_2\).;...; tương tự, \(A_{i-1}A_i;A_{i+1}A_{i+2}\) cắt nhau tại điểm \(B_i\) (xem \(A_7\) là \(A_1\) và \(A_8\) là \(A_2\)). Chứng minh rằng tổng diện tích của sáu tam giác \(A_iB_iA_{i+1}\), \(i=1,...,6\) không bé hơn 1.
H24
Giải mục 1 trang 113, 114 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 21:05
Cho hình hộp \(ABCD.A'B'C'D'\) và một mặt phẳng \(\left( \alpha \right)\) cắt các mặt của hình hộp theo các giao tuyến \(MN,NP,PQ{\rm{,}}QR,RS,SM\) như Hình 18. Chứng minh các cặp cạnh đối của lục giác \(MNPQRS\) song song với nhau.
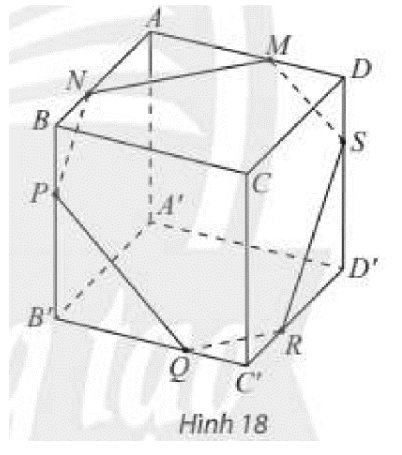
Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)
Đúng 0
Bình luận (0)