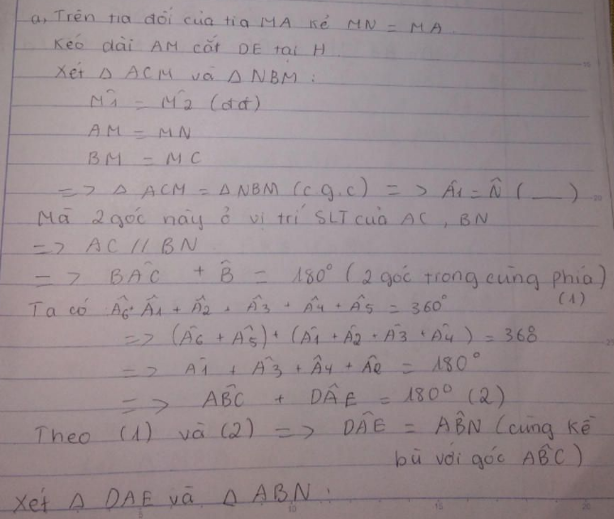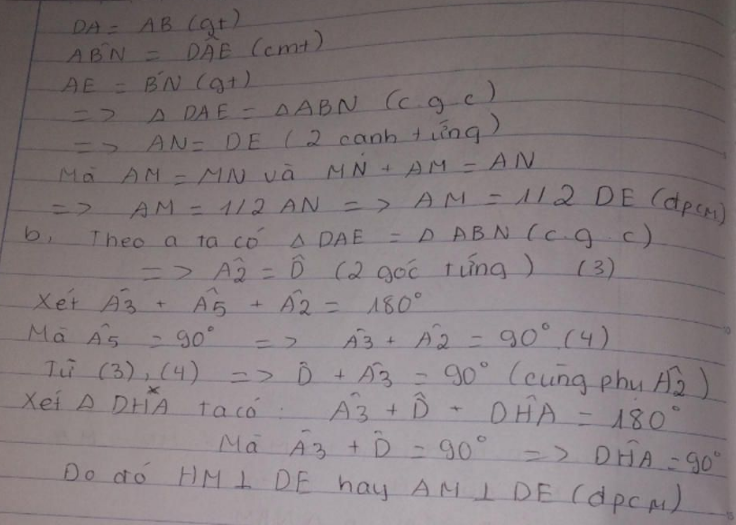Trên nửa mặt phẳng bờ AB chứa điểm C,vẽ Ax//BC. Chứng ming : góc ABC bằng góc
CAx
NN
Những câu hỏi liên quan
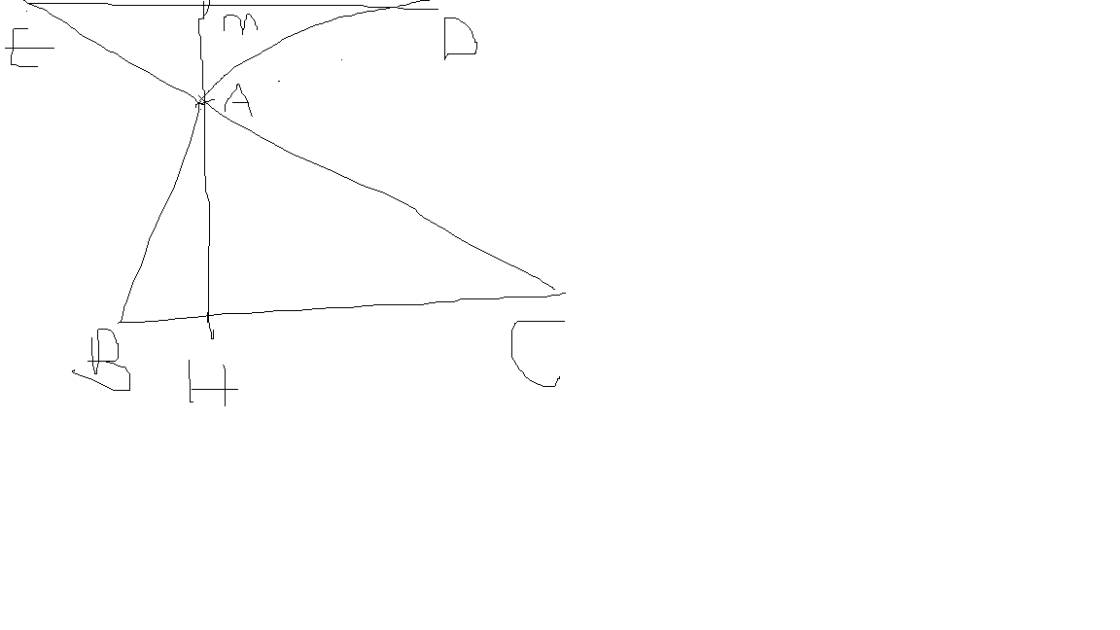
Cho ∆ABC có AB=AC. Tia phân giác góc A cắt cạnh BC tại D. a) Chứng minh: ∆ABD=∆ACD ; AD vuông góc với BC. b) Trên nửa mặt phẳng bờ AB chứa điểm C,vẽ Ax//BC. Chứng ming : góc ABC bằng góc CAx. c) Trên tia Ax lấy điểm K sao cho AK=BD. Gọi I là trung điểm của AC. Chứng minh I là trung điểm của DK.
a: Xét ΔBAD và ΔCAD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Đúng 0
Bình luận (0)
Cho tam giác ABC trên nửa mặt phẳng bờ AB không chứa điểm C. Vẽ tia Ax sao cho góc xAB bằng góc ABC. Trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ Ay sao cho góc yAC = ABC. Vẽ Ah vuông góc với BC. Chứng minh rằng Ah vuông góc với Ax.
Mấy bạn vẽ hình cho mình thì càng tốt nhé!
giải thích một số từ viết tắt:tam giác(tg) , góc (g)
TH1: tia Ax và AC nằm ở 2 nửa mặt phẳng đối nhau bờ là BA. CÒn tia Ay và AB nằm 2 nwả mặt phẳng bờ đối nhau bờ là AC:
TRên tia MA lấy điểm I sao cho MI=MA. tg BAM=tg CIM(c.g.c) => g ABM=gMCI=> gACI=gACM+gBAM=180- g BAC và BA=CI
LẠi có gDAE=180-gBAC nên gACI=gDAE. Dễ dàng chứng minh được tgACI=tgEAD(c.g.c)=>DE=AI=2AM
TH2: tia Ax và AC nằm cùng phía đối với BA. Còn BA và AE cùng phía đối với AC.trên tia đối MA lấy K sao cho KM=KA
Kéo dài BC nó sẽ cắt EA ở I gEAB= gABC-gAIB=gABC-90-gACB . tg EAB=tgCAD(c.g.c)=>gEAB+gDAC
TA có : gEAD=(gEAB+gDAC)+gBAC=(gABC-90-gACB)2+(1... =gB+gC=gBCK+gACM=gACK.Chứng minh tg ACK=tgEAD(c.g.c)=>AK=ED=2AM.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc tại B. trên cùng nửa mặt phẳng bờ chứa tia AC chứa điểm B vẽ tại tia Ax, Cy sao cho góc xAB=30 độ ,góc BCy=60 độ. Tìm kết luận
Cho
△
A
B
C
, trên nửa mặt phẳng bờ AC không chứa điểm, vẽ tia Ax sao cho
C
A
x
^
A
C
B
^
. Trên nửa mặt phẳng bờ AB không chứa điểm C, vẽ tia Ay sao cho
B
A
y
^...
Đọc tiếp
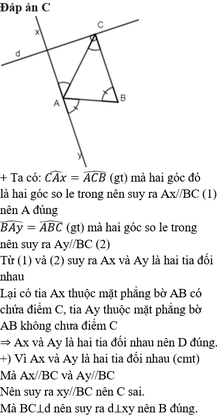
Cho △ A B C , trên nửa mặt phẳng bờ AC không chứa điểm, vẽ tia Ax sao cho C A x ^ = A C B ^ . Trên nửa mặt phẳng bờ AB không chứa điểm C, vẽ tia Ay sao cho B A y ^ = A B C ^ . Qua C kẻ đường thẳng d vuông góc với BC. Chọn câu sai
A. Ax//BC
B. d ⊥ xy
C. xy ⊥ BC
D. Ax và Ay là hai tia đối nhau
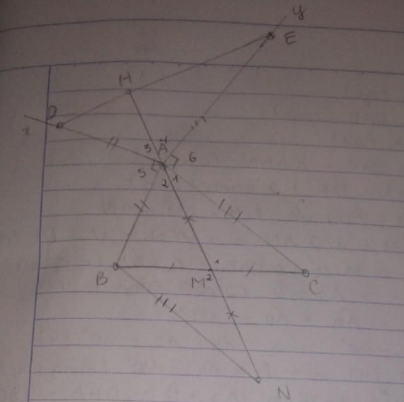
Cho tam giác ABC có góc A tù. Trên nửa mặt phẳng bờ AB không chứa điểm C vẽ tia Ax vuông góc với AB, trên tia Ax lấy điểm D sao cho AD = AB. Trên nửa mặt phẳng bờ AC không chứ điểm b vẽ Ay vuông góc với AC, trên tia Ay lấy điểm E sao cho AE=AC. Gọi M là trung điểm cạnh BC. Chứng minh rằng 2AM=DE
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE=AC. Chứng minh rằng:
a) AM=DE/2
b)AM vuông góc DE
Cho tam giác ABC. M là trung điểm của BC. Trên nửa mặt phẳng không chứa C có bờ AB, vẽ tia Ax vuông góc với AB, trên tia đó lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng không chứa B có bờ AC, vẽ tia Ay vuông góc với AC, trên tia đó lấy điểm E sao cho AE=AC. Chứng minh rằng:
a) AM=DE/2
b)AM vuông góc DE
:Cho tam giác ABC nhọn. Trên nửa mặt phẳng bờ AC ko chứa B, vẽ tia Ax vuông góc với AC. Trên nửa mặt phẳng bờ AB ko chứa C, vẽ tia Ay vuông góc với AB.Trên tia Ax lấy điểm D sao cho AD=AC. Trên tia Ay lấy điểm E sao cho AE=AB.Kẻ AH cắt BC tại H. Tia đối của AH cắt ED tại M ME=MD
Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB chứa C, vẽ tia Ax vuông góc AB;trên nửa mặt phẳng bờ AC chứa B, vẽ tia Ấy vuông góc AC. Lấy điểm D thuộc tia Ax sao cho AD=AB, điểm E thuộc tia Ấy sao cho AE=AC. Gọi M là Trung điểm BC. Chứng minh: AM vuông góc với DE, AM=1/2DE
cho tam giác ABC có góc A<90 độ. Trên nửa mặt phẳng bờ AB chứa điểm C vẽ tia Ax vuông góc với AB, trên tia Ax lấy D sao cho AD=AB. Trên nửa mặt phẳng bờ AC có chứa B vẽ tia Ay vuông góc với AC, trên tia Ay lấy E sao cho AE=AC. Gọi M là trung điểm của BC. CM:AM=DE/2
Xem thêm câu trả lời