Chứng minh: Với a; b; c dương (a+b+c)(1/a+1/b+1/c) lớn hơn hoặc bằng 9
H24
Những câu hỏi liên quan
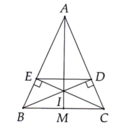
Cho▵ABC cân tại A. Kẻ tia AH vuông góc với BC ( H thuộc BC)
a) Chứng minh▵AHB =▵AHC
b) Chứng minh HB = HC
c) Kẻ IH vuông góc với AB tại I, HK vuông góc với AC tại K. Chứng minh▵AIK là tam giác cân d) Chứng minh IK // BC e) Chứng minh AH là đường trung trực của đoạn thẳng IK
a) Ta xét ▵AHB và▵AHC, ta có
AH là cạnh chung
AC=AB ( vì tam giác cân tại A)
góc AHC = góc AHB là góc vuông (90 độ)
-> ▵AHB =▵AHC (cạnh huyền- cạnh góc vuông)
b) Ta có ▵AHB =▵AHC (cmt)
->HB=HC ( 2 cạnh tương ứng)
c) Ta xét ▵AKH và ▵AIH. Ta có:
AH là cạnh chung
góc AKH = góc AIK = 90 độ
-> ▵AKH =▵AIH (cạnh huyền - cạnh góc vuông)
-> AK = AI (2 cạnh tương ứng) nên ▵AIK là tam giác cân và cân tại A
d) Ta áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ta có AH là cạnh chung cùng vuông góc với IK và BC
-> IK // BC
e) Ta cho giao điểm của AH và IK là O
Ta xét ▵AKO và ▵AIO
Ta có AK=AI (cmt)
Góc AOK = góc AOI = 90 độ
-> ▵AKO = ▵AIO
-> KO = IO ( 2 cạnh tương ứng) -> AH là đường trung trực của đoạn thẳng IK
Đúng 2
Bình luận (0)
a) chứng minh a song song với b
b) chứng minh c vuông góc với b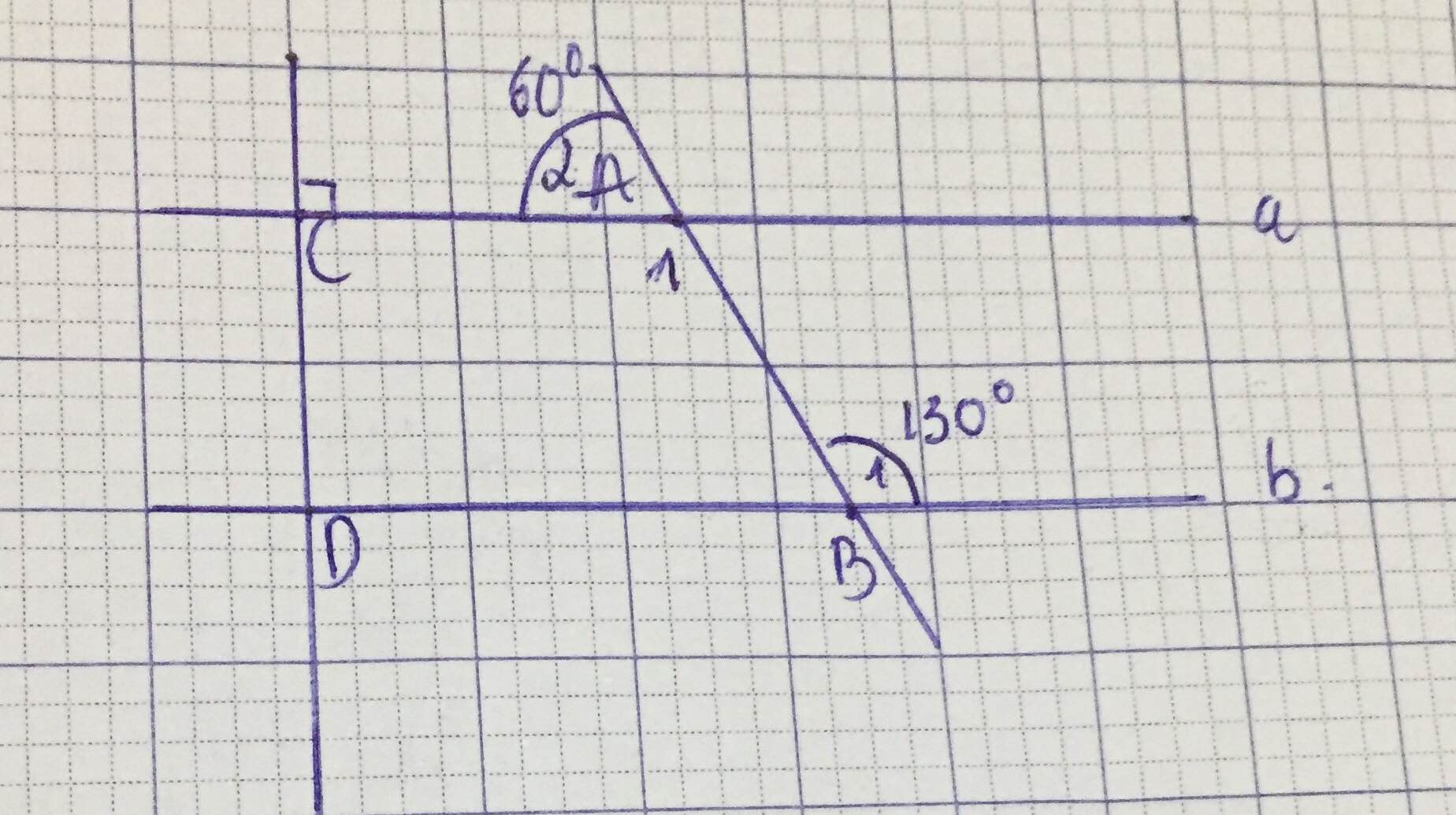
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A (A< 90 độ) Kẻ BD vuông góc với AC tại D , kẻ CE Vuông góc với AB tại E:
a,Chứng minh Δ ABD cân
b,Chứng minh DE song song với BC
c,Gọi I là giao điểm của BD và CE . Chứng minh IB=IC
d,Chứng minh AI vuong góc với BC
a: Xét ΔADB vuông tại Dvà ΔAEC vuông tại E có
AB=AC
góc A chung
Do đó: ΔADB=ΔAEC
=>AD=AE
b: Xét ΔABC co AE/AB=AD/AC
nên ED//BC
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
d: AB=AC
IB=IC
Do đó: AI là trung trực của BC
=>AI vuông góc với BC
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a gọi h là trung điểm của bc
a, Chứng minh AH vuông góc với BC
b, Kẻ HE vuong góc với AB tại E ; HF vuông góc với AC tại F . Chứng minh HE = HF
c, Chứng minh tam giác AEF là tam giác cân
d, Chứng minh EF song song BC
Cho tam giác ABC cân tại A
A
^
90
°
. Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E.a) Chứng minh tam giác ADE cân.b) Chứng minh DE// BC.c) Gọi I là giao điểm của BD và CE. Chứng minh IB ICd) Chứng minh.
A
I
⊥
B
C
.
Đọc tiếp
Cho tam giác ABC cân tại A A ^ < 90 ° . Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E.
a) Chứng minh tam giác ADE cân.
b) Chứng minh DE// BC.
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC
d) Chứng minh. A I ⊥ B C .
Cho a>2, b>2.
a) Chứng minh a.b > a+b
b) Chứng minh a^2+b^2+c^2 ≥ ab+bc+ca
c) Chứng minh a^2+b^2+c^2+3 ≥ 2.(a+b+c)
d) Chứng minh a^2+b^2 ≥ 1/2 với a+b=1
e) Chứng minh a^2+b^2+c^2 ≥ 1/3 với a+b+c=1
Cho tam giác ABC cân tại A ( Góc A nhọn ). Kẻ BD vuông góc với AC tại D; Kẻ CE vuông góc với AB tại E
a, Chứng minh tam giác ADE cân
b, Chứng minh DE song song với BC
c, Gọi I là giao điểm của BD và CE, chứng minh IB = IC
d, Chứng minh AI vuông góc với BC
cho tam giác ABC cân ở A (góc A nhỏ hơn 90 độ) kẻ AK vuông góc với CK
a chứng minh BK=CK
b kẻ KE vuông góc với AB,KF vuông góc với ACchứng minh tam giác KEB=tam giácKFC
c,chứng minh AK là phân giác của góc BAC
d,chứng minh EF=BC
a) Xét tam giác ABC cân tại A:
AK là đường cao \(\left(AK\perp BC\right).\)
\(\Rightarrow\) AK là đường trung tuyến (Tính chất tam giác cân).
\(\Rightarrow\) BK = CK.
b) Tam giác ABC cân tại A (gt).
\(\Rightarrow\widehat{B}=\widehat{C}\) (Tính chất tam giác cân).
Xét tam giác KEB vuông tại E và tam giác KFC vuông tại F:
\(\widehat{B}=\widehat{C}\left(cmt\right).\)
BK = CK (cmt).
\(\Rightarrow\) Tam giác KEB = Tam giác KFC (cạnh huyền - góc nhọn).
c) Xét tam giác ABC cân tại A:
AK là đường cao \(\left(AK\perp BC\right).\)
\(\Rightarrow\) AK là phân giác của góc BAC (Tính chất tam giác cân).
Đúng 1
Bình luận (0)
Tập hợp các điểm K thỏa mãn là đường tròn đường kính AC, BK=CK chỉ tại điểm E là trung điểm của BC như trên hình.
Vui lòng duc nguyen xem lại đề bài giúp mình.
Đúng 0
Bình luận (0)
Cho △ABC cân tại A. Kẻ BD vuông góc với AC tại D và CE vuông góc với AB tại E. Gọi I là giao điểm của BD và CE. a) Chứng minh: △ABD = △ACE. b) Chứng minh: IB = IC. c) Lấy M là trung điểm của AI. Chứng minh MB = MC. d) Chứng minh AI vuông góc với BC
( CẦN GẤP!!!!!!!!!!!!!!!!!!!!!!!!!!!)
Bài 2: Cho ∆ABC cân tại A (𝐴̂ 900 ). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E .a) Chứng minh ∆ADE cân ;b) Chứng minh DE // BC;c) Gọi I là giao điểm của BD và CE. Chứng minh IB IC;d) AI cắt BC tại K. Chứng minh AK vuông góc với BC.Bài 3: Cho ∆ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD CE. Gọi I là giao điểm của BE và CD.a) Chứng minh ∆BDE ∆CED;b) Chứng minh IB IC, ID IE;c) Chứng minh DE // BC;d) Gọi M là trung điểm của...
Đọc tiếp
Bài 2: Cho ∆ABC cân tại A (𝐴̂ < 900 ). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E .
a) Chứng minh ∆ADE cân ;
b) Chứng minh DE // BC;
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC;
d) AI cắt BC tại K. Chứng minh AK vuông góc với BC.
Bài 3: Cho ∆ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh ∆BDE = ∆CED;
b) Chứng minh IB = IC, ID = IE;
c) Chứng minh DE // BC;
d) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Bài 2:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hayΔADE cân tại A
b: Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
=>AK là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao
Đúng 0
Bình luận (0)