có tớ làm rùi

Dạy tớ với.ban phạm trung hieu oi

khtn là gì

Ta có :

\(\left|2x-1\right|\ge0\)

\(\Rightarrow1+\left|2x-1\right|\ge1\)

\(\Rightarrow\frac{2}{1+\left|2x-1\right|}\le\frac{2}{1}=2\)

\(\Rightarrow1+\frac{2}{1+\left|2x-1\right|}\le3\)

\(\Rightarrow B_{max}=3\)

\(\Leftrightarrow\left|2x-1\right|=0\)

\(\Leftrightarrow2x-1=0\)

\(\Leftrightarrow2x=1\)

\(\Leftrightarrow x=\frac{1}{2}\)

Vậy ...

Để B lớn nhất thì 2/1 + |2x - 1| lớn nhất

=> 1 + |2x - 1| nhỏ nhất

Mà 1 + |2x - 1| < hoặc = 1

Dấu" ="  xảy ra khi và chỉ khi |2x - 1| = 0

=> 2x - 1 = 0

=> 2x = 1

=> x = 1/2

Vậy với x = 1/2 thì B lớn nhất = 1 + 2/1+1 = 1 + 1 = 2

\(ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow4\sqrt{2x-1}+3\sqrt{2x-1}=4\\ \Leftrightarrow\sqrt{2x-1}=\dfrac{4}{7}\\ \Leftrightarrow2x-1=\dfrac{16}{49}\\ \Leftrightarrow x=\dfrac{65}{98}\left(tm\right)\)

\(\sqrt{32x-16}+\sqrt{18x-9}=4\) (ĐKXĐ: x≥\(\dfrac{1}{2}\))

⇔ \(\sqrt{16\left(2x-1\right)}+\sqrt{9\left(2x-1\right)}=4\)

⇔ 4\(\sqrt{2x-1}\)\(+3\sqrt{2x-1}\)= 4

⇔ 7\(\sqrt{2x-1}=4\)

⇔ \(\sqrt{2x-1}=\dfrac{4}{7}\)

⇔ \(2x-1=\dfrac{16}{49}\)

⇔ 2x = \(\dfrac{65}{49}\)

⇔ x = \(\dfrac{65}{98}\) (TM)

Vậy x = \(\dfrac{65}{98}\)

1. Don't => doesn't

2. those => that

3. much => many

1. Chủ ngữ là "my mother" = "she" => phải dùng doesn't nha

2. "skirt" ở số ít nên phải dùng "that", "those" + danh từ số nhiều nha

3. "egg" là danh từ đếm được nên phải dùng "many", "much" dùng với danh từ không đếm được

Tham khảo ạ

                     Học sinh trung học cơ sở nên mặc quần áo bình thường

Mặc quần áo bình thường:

 - làm cho học sinh cảm thấy thoải mái.

 - cho học sinh tự do lựa chọn (kích cỡ, màu sắc, và kiểu dáng, v.v)

 - tạo cho học sinh cảm giác tự tin khi diện những bộ quần áo yêu thích.

 - làm cho trường học đầy màu sắc và sống động

\(1,\\ a,=3x\left(1-3y\right)\\ b,=9xy\left(2xy-x^2+4y\right)\\ c,=\left(x-y\right)\left(15x-5y\right)=5\left(x-y\right)\left(3x-y\right)\\ 2,\\ a,\Rightarrow2x^2\left(x^2-4\right)=0\Rightarrow2x^2\left(x-2\right)\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\\ b,\Rightarrow\dfrac{2}{5}x\left(x+10\right)-\left(x+10\right)=0\\ \Rightarrow\left(x+10\right)\left(\dfrac{2}{5}x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-10\\\dfrac{2}{5}x=1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-10\\x=\dfrac{5}{2}\end{matrix}\right.\)

\(3,\)

\(a,\left\{{}\begin{matrix}AK=KD\\BI=IC\end{matrix}\right.\Rightarrow KI\) là đtb hình thang ABCD

\(b,\) Vì KI là đtb hình thang ABCD nên \(KI=\dfrac{AB+CD}{2}=\dfrac{17}{2}=8,5\left(cm\right)\)

\(c,\) \(\left\{{}\begin{matrix}AK=KD\\KE//AB\end{matrix}\right.\Rightarrow BE=ED\Rightarrow KE\) là đtb tam giác ABD

\(\Rightarrow KE=\dfrac{1}{2}AB=2,5\left(cm\right)\)

\(\left\{{}\begin{matrix}BI=IC\\IF//AB\end{matrix}\right.\Rightarrow AF=FC\Rightarrow IF\) là đtb tam giác ABC

\(\Rightarrow IF=\dfrac{1}{2}AB=2,5\left(cm\right)\)

Ta có \(EF=KI-KE-IF=8,5-2,5-2,5=3,5\left(cm\right)\)

2.2 Đề lỗi không dịch được

2.3 

\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)

\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)

Do \(x_1\) là nghiệm của pt nên ta có: 

\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)

Thế vào bài toán:

\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)

\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)

(Bản thân câu này đề bài cũng rất dở)

Chỉ cần bài 2 thôi, e cảm ơn 

a.

ĐKXĐ: \(x\ge\dfrac{1}{3}\)

\(9x^2-6x+1+2\sqrt{3x-1}+1=0\)

\(\Leftrightarrow\left(3x-1\right)^2+2\sqrt{3x-1}+1=0\)

Do \(\left\{{}\begin{matrix}\left(3x-1\right)^2\ge0\\2\sqrt{3x-1}\ge0\end{matrix}\right.\) ; \(\forall x\ge\dfrac{1}{3}\)

\(\Rightarrow\left(3x-1\right)^2+2\sqrt{3x-1}+1>0\)

Hay phương trình đã cho vô nghiệm

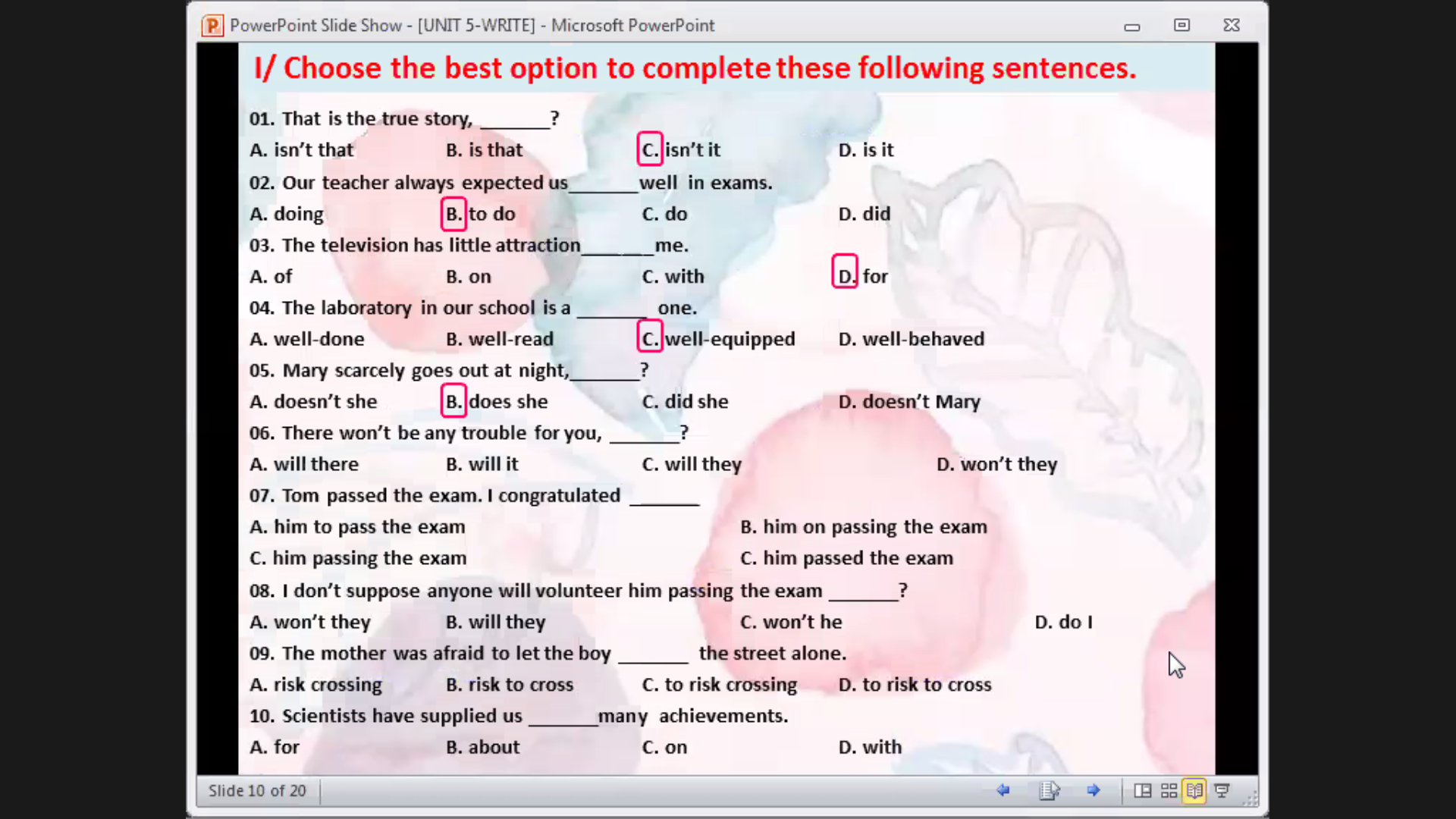
1 C

2 B

3 D

4 C

5 B

6 A

7 B

8 A

9 A

10 D