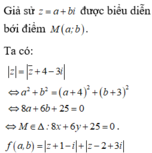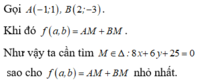Giá trị nhỏ nhất của A= I-x+7/3I+I-x-11/3I-17 là
CH
Những câu hỏi liên quan
tìm giá trị lớn nhất
C= 1- I2x -3I
D=I x -3I- I5-xI
tìm giá trị nhỏ nhất
A=1,5 +I2 -xI
B=I x -2002I+I x - 2001
Ta có : |2x - 3| \(\ge0\forall x\in R\)
Suy ra : 1 - |2x - 3| \(\le1\forall x\in R\)
=> Giá trị lớn nhất của biểu thức là 1 khi x = 3/2
Đúng 0
Bình luận (0)
Hãy tích cho tui đi
khi bạn tích tui
tui không tích lại bạn đâu
THANKS
Đúng 0
Bình luận (0)
tìm giá trị lớn nhất và nhỏ nhất của biểu thức:B=Ix-1I-Ix+3I với x< hoặc =7/11
Tìm giá trị nhỏ nhất của biểu thức sau:
B=I x-1I + I x-2I + Ix-3I + 2011
Ta có:
\(B-2011=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|\)
\(\ge x-1+0+3-x=2\)
\(\Rightarrow B-2011\ge2\)\(\Rightarrow B\ge2013\)
Dấu = khi \(\begin{cases}x-1\ge0\\x-2=0\\3-x\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge1\\x=2\\x\le3\end{cases}\)\(\Leftrightarrow x=2\)
Vậy MinB=2013 khi x=2
Đúng 0
Bình luận (0)
Xét các số phức z a +bi thỏa mãn đồng thời hai điều kiện
z
z
+
4
-
3
i
và
z
+
1
-
i
+
z...
Đọc tiếp
Xét các số phức z = a +bi thỏa mãn đồng thời hai điều kiện z = z + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2b là:
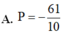
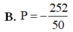
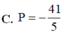
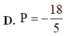
Tìm giá trị nhỏ nhất của A= Ix-1,5I-7,5+I2x-3I
chú ý: I là giá trị tuyệt đối
Ta có \(\hept{\begin{cases}\left|x-1,5\right|\ge0\forall x\\\left|2x-3\right|\ge0\forall x\end{cases}}\Rightarrow\left|x-1,5\right|+\left|2x-3\right|-7\ge-7\forall x\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-1,5=0\\2x-3=0\end{cases}\Rightarrow\hept{\begin{cases}x=1,5\\x=1,5\end{cases}}\Rightarrow x=1,5}\)
Vậy GTNN của A là - 7 khi x = 1,5
Xét các số phức z a + bi, (a,b
∈
R) thỏa mãn đồng thời hai điều kiện
z
z
¯
+
4
-
3
i
và
z
+
1...
Đọc tiếp
Xét các số phức z = a + bi, (a,b ∈ R) thỏa mãn đồng thời hai điều kiện z = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2b là:
A. P = - 61 10
B. P = - 252 50
C. P = - 41 5
D. P = - 18 5
Đáp án A.
Phương pháp:
Từ z = z ¯ + 4 - 3 i tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z = x + yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất ó MA = MB
Cách giải: Gọi z = x + ui ta có:
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất.
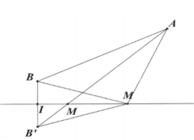
Ta có: 
dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có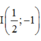 
và
A
B
→
=
3
;
-
4
Phương trình đường trung trực của AB là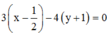 
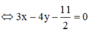
Để (MA + MB)min ó Tọa độ điểm M là nghiệm của hệ phương trình
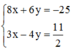
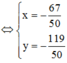
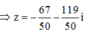
Đúng 0
Bình luận (0)
Xét các số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa mãn đồng thời hai điều kiện
z
z
¯
+
4
-
3
i
và
z...
Đọc tiếp
Xét các số phức z = a + b i a , b ∈ ℝ thỏa mãn đồng thời hai điều kiện z = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P = a + 2 b là:
A. P = - 252 50 .
B. P = - 41 5 .
C. P = - 61 10 .
D. P = - 18 5
Xét các số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
)
thỏa mãn đồng thời hai điều kiện
z
+
y
i...
Đọc tiếp
Xét các số phức z = a + b i ( a , b ∈ ℝ ) thỏa mãn đồng thời hai điều kiện z + y i = z ¯ + 4 - 3 i và z + 1 - i + z - 2 + 3 i đạt giá trị nhỏ nhất. Giá trị P=a+2b là:
A. P= - 61 10
B. P= - 252 50
C. P= - 41 5
D. P= - 18 5
Đáp án A.
Phương pháp:
Từ 
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
nhỏ nhất
Cách giải: Gọi z=x+ui ta có:
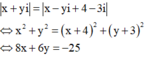
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
nhỏ nhất.
Ta có: 
Dấu bằng xảy ra 
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có 
Phương trình đường trung trực của AB là
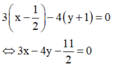
Để 
Tọa độ điểm M là nghiệm của hệ phương trình
Đúng 0
Bình luận (0)
Cho số phức
z
x
+
y
i
với
x
;
y
∈
R
thỏa mãn
z
-
1
-
i
≥
1
và
z
-
3
-
3
i
≤
5
....
Đọc tiếp
Cho số phức z = x + y i với x ; y ∈ R thỏa mãn z - 1 - i ≥ 1 và z - 3 - 3 i ≤ 5 . Gọi m; M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = x+2y. Tính tỉ số M m
A. 9 4
B. 7 2
C. 5 4
D. 14 5
