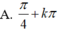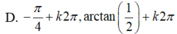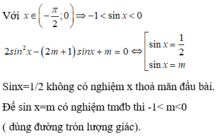Giải phương trình Sinx - √3sin(3π/2 - x) = 2sin2x
TL
Những câu hỏi liên quan
Giải các phương trình: 1 - cos x = sin x x ∈ π ; 3 π
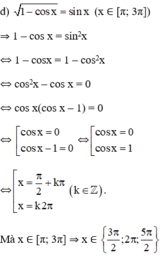
Thử lại: Trong 3 nghiệm trên thì nghiệm 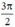 không thỏa mãn
không thỏa mãn
Đúng 0
Bình luận (0)
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình sau:
sin2x + sinx - 2sin2x + cosx +1 =0
sin2x + 1 - 2sin2x + sinx + cosx = 0
⇔ sin2x + cos2x + sinx + cosx = 0
⇔ \(\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)+\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=0\)
⇔ \(sin\left(2x+\dfrac{\pi}{4}\right)+sin\left(x+\dfrac{\pi}{4}\right)=0\)
⇔ \(2sin\left(\dfrac{3x}{2}+\dfrac{\pi}{4}\right).cos\dfrac{x}{2}=0\)
⇔ \(\left[{}\begin{matrix}sin\left(3x+\dfrac{\pi}{4}\right)=0\\cos\dfrac{x}{2}=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k.\dfrac{\pi}{3}\\x=\pi+k.2\pi\end{matrix}\right.\) , k ∈ Z
Đúng 0
Bình luận (0)
Giải phương trình
5
(
sin
x
+
sin
3
x
+
c
o
s
3
x
1
+
2
sin
2
x
)
cos
2
x
+
3
Đọc tiếp
Giải phương trình 5 ( sin x + sin 3 x + c o s 3 x 1 + 2 sin 2 x ) = cos 2 x + 3
![]()
![]()
![]()
![]()
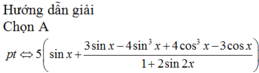
=cos2x+3

=cos2x+3 (*)
Ta có: 3( sin x – cosx) – 4 ( sin3x - cos3x)
= 3(sinx – cosx) – 4(sinx – cosx ).(sin2x + sinx. cosx+ cos2 x)
= 3( sin x – cosx) – 4(sinx – cosx).(1+ sinx. cosx)
= (sin x – cosx) . ( 3- 4 – 4sinx. cosx)
= ( sinx – cosx). (- 1- 4sinx. cosx) = - ( sinx – cosx)( 1+ 2sin2x)
Khi đó (*) trở thành
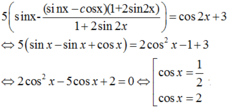
![]()
Đúng 0
Bình luận (0)
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Đúng 0
Bình luận (0)
Giải phương trình:
1,\(3sin^22x-2sin2x\times cos2x-4cos^22x=2\)
2,\(2\sqrt{3}cos^2x+6sinx\times cosx=3+\sqrt{3}\)
3,\(3cos^24x+5sin^24x=2-2\sqrt{3}sin4xcos4x\)
1.
\(3sin^22x-2sin2x.cos2x-4cos^22x=2\)
\(\Leftrightarrow-\dfrac{3}{2}\left(1-2sin^22x\right)-2sin2x.cos2x-2\left(2cos^22x-1\right)=\dfrac{5}{2}\)
\(\Leftrightarrow sin4x+\dfrac{7}{2}cos4x=-\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{53}}{2}\left(\dfrac{2}{\sqrt{53}}sin4x+\dfrac{7}{\sqrt{53}}cos4x\right)=-\dfrac{5}{2}\)
\(\Leftrightarrow sin\left(4x+arccos\dfrac{2}{\sqrt{53}}\right)=-\dfrac{5}{\sqrt{53}}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+arccos\dfrac{2}{\sqrt{53}}=arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\\4x+arccos\dfrac{2}{\sqrt{53}}=\pi-arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}+\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}-\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (2)
2.
\(2\sqrt{3}cos^2x+6sinx.cosx=3+\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}\left(2cos^2x-1\right)+6sinx.cosx=3\)
\(\Leftrightarrow\sqrt{3}cos2x+3sin2x=3\)
\(\Leftrightarrow2\sqrt{3}\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)=3\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\pi\end{matrix}\right.\)
Đúng 3
Bình luận (0)
3.
\(3cos^24x+5sin^24x=2-2\sqrt{3}sin4x.cos4x\)
\(\Leftrightarrow4cos^24x+4sin^24x-cos^24x+sin^24x=2-2\sqrt{3}sin4x.cos4x\)
\(\Leftrightarrow4-cos8x=2-\sqrt{3}sin8x\)
\(\Leftrightarrow cos8x-\sqrt{3}sin8x=2\)
\(\Leftrightarrow\dfrac{1}{2}cos8x-\dfrac{\sqrt{3}}{2}sin8x=1\)
\(\Leftrightarrow cos\left(8x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow8x+\dfrac{\pi}{3}=k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{24}+\dfrac{k\pi}{4}\)
Đúng 3
Bình luận (0)
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m 0 có nghiệm
x
∈
-
π
2
;
0
A. – 1 m 0 B. 1 m 2 C. – 1 m 0 D. 0 m 1
Đọc tiếp
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m = 0 có nghiệm x ∈ - π 2 ; 0
A. – 1< m < 0
B. 1< m< 2
C. – 1< m< 0
D. 0< m< 1
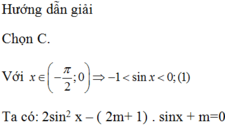
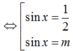
Phương trình sinx = 1/2 không có nghiệm x ∈ - π 2 ; 0
Nên để phương trình đã cho có nghiệm x ∈ - π 2 ; 0 khi và chỉ khi phương trình sinx = m có nghiệm trên khoảng đó. Kết hợp với (*) suy ra -1< m< 0
Đúng 0
Bình luận (0)
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m 0 có nghiệm x ∈ (
-
π
2
; 0). A. -1 m B. 1 m C. -1 m 0 D. 0 m 1
Đọc tiếp
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( - π 2 ; 0).
A. -1 < m
B. 1 < m
C. -1 < m < 0
D. 0 < m < 1
Phương trình
2
sin
2
x
+
sin
x
cos
x
-
cos
2
x
0
có nghiệm là:
Đọc tiếp
Phương trình 2 sin 2 x + sin x cos x - cos 2 x = 0 có nghiệm là: