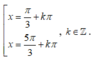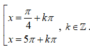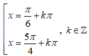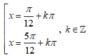1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
4, \(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\) . ĐKXĐ : sin2x ≠ 0
⇒ sin2x . cosx + 2sinx + sin2x . sinx + 2cosx = \(\dfrac{10sin2x}{3}\) (x sin2x)
⇔ sin2x . (sinx + cosx) + 2 (sinx + cosx) = \(\dfrac{10sin2x}{3}\)
⇔ (sinx + cosx) . (sin2x + 2) = \(\dfrac{10sin2x}{3}\)
Đặt a = sinx + cosx = \(\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)\). Điều kiện của a là \(a\in\left[-\sqrt{2};\sqrt{2}\right]\)
⇒ a2 = sin2x + cos2x + 2sinx . cosx = 1 + sin2x
⇒ sin2x = a2 - 1
Đặt như vậy ta được hệ phương trình :
\(\left\{{}\begin{matrix}a\left(a^2-1+2\right)=\dfrac{10}{3}\left(a^2-1\right)\\-\sqrt{2}\le a\le\sqrt{2}\end{matrix}\right.\)
⇔ \(a=\dfrac{2-\sqrt{19}}{3}\)
Vậy phương trình đã cho tương đương
\(sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{2-\sqrt{19}}{3\sqrt{2}}\)
4.
ĐK: \(x\ne\dfrac{k\pi}{2}\)
Đặt \(cosx+sinx=t\left(t\in\left[-\sqrt{2};\sqrt{2}\right]\right)\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\).
\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
\(\Leftrightarrow cosx+sinx+\dfrac{cosx+sinx}{cosx.sinx}=\dfrac{10}{3}\)
\(\Leftrightarrow t+\dfrac{t}{\dfrac{t^2-1}{2}}=\dfrac{10}{3}\)
\(\Leftrightarrow3t\left(t^2-1\right)+6t=10\left(t^2-1\right)\)
\(\Leftrightarrow3t^3-10t^2+3t+10=0\)
\(\Leftrightarrow\left(t-2\right)\left(3t^2-4t-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\\t=\dfrac{2+\sqrt{19}}{3}\\t=\dfrac{2-\sqrt{19}}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\left(l\right)\\t=\dfrac{2+\sqrt{19}}{3}\left(l\right)\\t=\dfrac{2-\sqrt{19}}{3}\end{matrix}\right.\)
\(\Leftrightarrow t=\dfrac{2-\sqrt{19}}{3\text{}}\)
\(\Leftrightarrow sinx+cosx=\dfrac{2-\sqrt{19}}{3\text{}}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{2-\sqrt{19}}{3\sqrt{2}\text{}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(\dfrac{2-\sqrt{19}}{3\sqrt{2}\text{}}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(\dfrac{2-\sqrt{19}}{3\sqrt{2}\text{}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(\dfrac{2-\sqrt{19}}{3\sqrt{2}\text{}}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(\dfrac{2-\sqrt{19}}{3\sqrt{2}\text{}}\right)+k2\pi\end{matrix}\right.\)