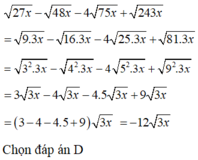3x3 - 48x = 0
H24
Những câu hỏi liên quan
Bài 2 : Tìm x biết:a) 2x(x – 5) – x(3 + 2x) 26 b) 5x(x – 1) x – 1 c) 2(x + 5) - x2 – 5x 0 d) (2x – 3)2 - (x + 5)20e) 3x3 – 48x 0 f) x3 + x2 – 4x 4g) (x – 1)(2x + 3) – x(x – 1) 0 h) x2 – 4x + 8 2x – 1Bài 3: Sắp xếp rồi làm tính chia:a) b) Bài 4: Tìm a sao cho a) Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5b) Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.Bài 5*:...
Đọc tiếp
Bài 2 : Tìm x biết:
a) 2x(x – 5) – x(3 + 2x) = 26 b) 5x(x – 1) = x – 1
c) 2(x + 5) - x2 – 5x = 0 d) (2x – 3)2 - (x + 5)2=0
e) 3x3 – 48x = 0 f) x3 + x2 – 4x = 4
g) (x – 1)(2x + 3) – x(x – 1) = 0 h) x2 – 4x + 8 = 2x – 1
Bài 3: Sắp xếp rồi làm tính chia:
a) ![]()
b) ![]()
Bài 4: Tìm a sao cho
a) Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5
b) Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Bài 5*: Chứng minh rằng biểu thức:
A = x(x - 6) + 10 luôn luôn dương với mọi x.
B = x2 - 2x + 9y2 - 6y + 3 luôn luôn dương với mọi x, y.
Bài 6* : Tìm GTLN (GTNN) của biểu thức sau :
A = x2 – 4x + 2019 B = 4x2 + 4x + 11
C = 4x – x2 +1 D = 2020 – x2 + 5x
E = (x – 1)(x + 3)(x + 2)(x + 6) F= - x2 + 4xy – 5y2 + 6y – 17
G = x2 – 4xy + 5y2 + 10x – 22y + 28
Bài 7: Cho biểu thức M = ![]()
a/ Tìm điều kiện để biểu thức M có nghĩa ?
b/ Rút gọn biểu thức M ?
c/ Tìm x nguyên để M có giá trị nguyên.
d/ Tìm giá trị của M tại x = -2
e/ Với giá trị nào của x thì M bằng 5.
Bài 8 : Cho biểu thức : M = ![]()
a) Tìm điều kiện xác định và rút gọn biểu thức
b) Tính giá trị của M khi x = 1; x = -1
c) Tìm số tự nhiên x để M có giá trị nguyên.
Bài 9: Cho biểu thức ![]()
a/Tìm giá trị của x để giá trị của biểu thức C được xác định.
b/Tìm x để C = 0.
c/ Tính giá trị của C biết |2x -1| = 3
d/ Tìm x để C là số nguyên âm lớn nhất.
Bài 2:
a: \(\Leftrightarrow2x^2-10x-3x-2x^2=26\)
=>-13x=26
hay x=-2
b: \(\Leftrightarrow\left(x-1\right)\left(5x-1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{5}\right\}\)
c: \(\Leftrightarrow\left(x+5\right)\left(2-x\right)=0\)
hay \(x\in\left\{-5;2\right\}\)
Đúng 0
Bình luận (0)
\(3x^3-48x=0\)
\(3x^3-48x=0\)
\(3x^3-48x=0\)
\(3x\cdot\left(x^2-16\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=0\\x^2-16=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=\left\{\pm4\right\}\end{cases}}\)
Vậy,............
Đúng 0
Bình luận (0)
Tìm x biết
x
3
–
12
x
2
+
48
x
–
64
0
A. x -4 B. x 4 C. x -8 D. x 8
Đọc tiếp
Tìm x biết x 3 – 12 x 2 + 48 x – 64 = 0
A. x = -4
B. x = 4
C. x = -8
D. x = 8
Ta có
x 3 – 12 x 2 + 48 x – 64 = 0 ⇔ x 3 – 3 . x 2 . 4 + 3 . x . 4 2 – 4 3 = 0 ⇔ ( x – 4 ) 3 = 0
ó x – 4 = 0 ó x = 4
Vậy x = 4
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
\(48x^2-22x+3=0\)
tìm x:
x^2-48x-25=0
\(\Delta=b^2-4ac=\left(-48\right)^2-4.1.\left(-25\right)=2400>0\)
do đó pt có 2 nghiệm phân biệt là:
\(•x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{48-\sqrt{2400}}{2}=24-10\sqrt{6}\\ •x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{48+\sqrt{2400}}{2}=24+10\sqrt{6}\)
Đúng 0
Bình luận (0)
\(x^2-48x-25=0\)
\(\Leftrightarrow x^2-2.x.24+24^2-601=0\)
\(\Leftrightarrow\left(x-24\right)^2-601=0\)
\(\Leftrightarrow\left(x-24\right)^2=601\)
\(\Leftrightarrow x-24=\sqrt{601}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-24=\sqrt{601}\\x-24=-\sqrt{601}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=24+\sqrt{601}\\x=24-\sqrt{601}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3x3-75x=0
\(3x^3-75x=0\Leftrightarrow3x\left(x^2-25\right)=0\Leftrightarrow3x\left(x-5\right)\left(x+5\right)=0\Leftrightarrow x=0;x=-5;x=5\)
Đúng 2
Bình luận (0)
x3+3x3+2x=0
\(x^3+3x^2+2x=0\)
\(\Leftrightarrow x\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
x4+3x3-x-3=0
\(x^4+3x^3-x-3=0\)
\(\Leftrightarrow x^3\left(x+3\right)-\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^3-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^3-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Vậy \(x\in\left\{-3;1\right\}\)
Đúng 3
Bình luận (0)
Rút gọn biểu thức
27
x
-
48
x
-
4
75
x
+
243
x
với x
≥
0 ta được kết quả là: A. 403x B.
28
x
C.
39
x
D.
−
12
3
x
Đọc tiếp
Rút gọn biểu thức 27 x - 48 x - 4 75 x + 243 x với x ≥ 0 ta được kết quả là:
A. 403x
B. 28 x
C. 39 x
D. − 12 3 x