Ai giúp em câu này ik, em cảm ơn.
HT
Những câu hỏi liên quan
Có ai giúp em câu này với em cảm ơn.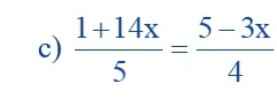
Lời giải:
$\frac{1+14x}{5}=\frac{5-3x}{4}$
$\Rightarrow 4(1+14x)=5(5-3x)$
$4+56x=25-15x$
$56x+15x=25-4$
$71x=21$
$x=\frac{21}{71}$
Đúng 1
Bình luận (0)
c, \(\Rightarrow4+56x=25-15x\Leftrightarrow71x=21\Leftrightarrow x=\dfrac{21}{71}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời

Có ai giúp em câu này với em cảm ơn.
số hs khá là: \(\dfrac{3}{4}\times\dfrac{1}{6}=\dfrac{1}{8}\left(hs\right)\)
a: số hs lớp 6A là : \(\dfrac{3}{4}+\dfrac{1}{8}+5=\dfrac{18}{24}+\dfrac{3}{24}+5=5\dfrac{21}{24}=5\dfrac{7}{8}=\dfrac{47}{8}\left(hs\right)\)
b: tỉ số là : \(\dfrac{3}{4}\times100:\dfrac{1}{8}=\dfrac{300}{4}:\dfrac{1}{8}=\dfrac{300\times8}{4\times1}=600\%\)
Đúng 1
Bình luận (1)
Gọi học sinh lớp 6a là x hs
Số học sinh giỏi là : \(\dfrac{3}{4}x\)(hs)
Số học sinh khác là : \(\dfrac{1}{6}.\dfrac{3}{4}x=\dfrac{1}{8}x\) (hs)
Theo bài ra có :
\(x-\dfrac{3}{4}x-\dfrac{1}{8}x=5\)
\(x\left(1-\dfrac{3}{4}-\dfrac{1}{8}\right)=5\)
\(\dfrac{1}{8}x=5\)
\(x=40\)
Vậy số hcj sinh lớp 6a là 40 hs
Số học sinh giỏi là : \(\dfrac{3}{4}.40=30\) (hs)
Số học sinh khá là :\(\dfrac{1}{6}.30=5\) (hs)
ĐS ...
Đúng 0
Bình luận (0)
Ai giúp em câu này với em cảm ơn nhiều.
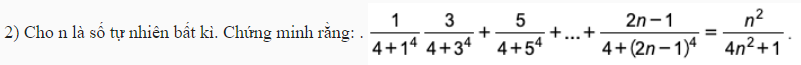
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
Đúng 0
Bình luận (0)
có ai giúp em câu này với ạ em cảm ơn.
Ai giúp em câu này với em cảm ơn nhiều ạ!
Đọc tiếp
Ai giúp em câu này với em cảm ơn nhiều ạ!
a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Đúng 6
Bình luận (1)
Em vẫn còn băn khoăn về câu này ấy ạ, nên ai đó giúp em câu này với em cảm ơn ạ.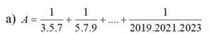
A = 1/3.5.7 + 1/5.7.9+ ... + 1/2019.2021.2023
2A = 2/3.5.7 + 2/5.7.9+ ... + 2/2019.2021.2023
2A = 1/3-1/5+1/7+1/5-1/7+1/9+....+1/2019-1/2021+1/2023
2A = 1/3 - 1/2023
2A = 2023/6069 - 3/6069
2A = 2023-3/6069
2A = 2020/6069
A = 1010/6069
Vậy A = 1010/6069
Đúng 0
Bình luận (0)
Ai giúp em câu này với ạ :(( em cảm ơn nhiều nhaaaaaa
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
Ai giúp em 2 câu này với em cảm ơn nhiều ạ!

Giải hpt:
Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)
Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Ai đó giúp em câu này với ạ em cảm ơn 🥺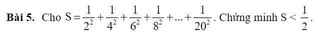
\(S=\dfrac{1}{2^2}+\dfrac{1}{\left(2.2\right)^2}+\dfrac{1}{\left(2.3\right)^2}+...+\dfrac{1}{\left(2.10\right)^2}\)
\(=\dfrac{1}{2^2}+\dfrac{1}{2^2.2^2}+\dfrac{1}{2^2.3^2}+...+\dfrac{1}{2^2.10^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{10^2}\right)\)
\(< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\right)\)
\(=\dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{4}\left(2-\dfrac{1}{10}\right)< \dfrac{1}{4}.2=\dfrac{1}{2}\) (đpcm)
Đúng 1
Bình luận (0)





